Question

已知P：|1-

x-1

3

|≤2，Q：x2-2x+1-m2≤0(m＞0)，又知非P是非Q的必要非充分条件，则m的取值范围是______．

Answer 1

由|1-

x-1

3

|≤2，得|x-4|≤6，解得-2≤x≤10．即P：-2≤x≤10．
由x²-2x+1-m²≤0，得[x-（1-m）][x-（1+m）]≤0，
∵m＞0，
∴1-m＜1+m，
∴不等式的解为1-m≤x≤1+m，
即Q：1-m≤x≤1+m．
∵非P是非Q的必要不充分条件，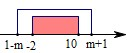
∴Q是P的必要不充分条件，
即

1-m≤-1 1+m≤6

，
解得

m≥2 m≤5

，即2≤m≤5．
∴m的取值范围是2≤m≤5．