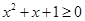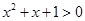题目内容
已知命题p:“?x∈[1,2]都有x2≥a”.命题q:“?x0∈R,使得x02+2ax0+2-a=0成立”,若命题“p∧q”是真命题,则实数a的取值范围为____________.
(-∞,-2]∪{1}
若p是真命题,即a≤(x2)min,x∈[1,2],所以a≤1;若q是真命题,即x02+2ax0+2-a=0有解,则Δ=4a2-4(2-a)≥0,即a≥1或a≤-2.命题“p∧q”是真命题,则p是真命题,q也是真命题,故有a≤-2或a=1.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
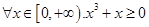 ”的否定是 ( )
”的否定是 ( )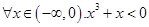
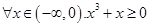
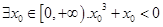
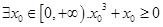
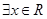 ,使
,使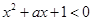 ”的否定是假命题,则实数
”的否定是假命题,则实数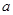 的取值范围是 .
的取值范围是 .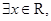 使得
使得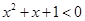 ”的否定是 ( )
”的否定是 ( )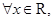 均有
均有