题目内容
11.已知cosx+siny=$\frac{1}{2}$,求z=asiny+cos2x,(a∈R)的最大值.分析 由已知把siny用含有x的三角函数代替,然后利用换元法结合二次函数求得z的最大值.
解答 解:∵cosx+siny=$\frac{1}{2}$,∴siny=$\frac{1}{2}$-cosx,
∴z=asiny+cos2x=$\frac{a}{2}$-acosx+cos2x,
∵-1≤siny≤1,∴-1≤$\frac{1}{2}$-cosx≤1,得-$\frac{1}{2}$≤cosx≤1,
令t=cosx,则$z={t^2}-at+\frac{a}{2}$$({-\frac{1}{2}≤t≤1})$,
对称轴$t=\frac{a}{2}$,①当$\frac{a}{2}≤\frac{1}{4}$,即$a≤\frac{1}{2}$时,${z_{max}}={1^2}-a+\frac{a}{2}=1-\frac{a}{2}$;
②当$\frac{a}{2}>\frac{1}{4}$,即$a>\frac{1}{2}$时,${z_{max}}={({-\frac{1}{2}})^2}+\frac{a}{2}+\frac{a}{2}=a+\frac{1}{4}$.
综上所述:${z_{max}}=\left\{\begin{array}{l}1-\frac{a}{2},a≤\frac{1}{2}\\ a+\frac{1}{4},a>\frac{1}{2}\end{array}\right.$.
点评 本题考查与三角函数有关的最值,考查了换元法,训练了二次函数最值的求法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知集合A={x|x2-x≤0},B={x|-2≤x≤0},则A∩∁RB=( )
| A. | ∅ | B. | {x∈R|x≠0} | C. | {x|0<x≤1} | D. | R |
2.有如下命题:命题p:设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;命题q:“?x0∈R,x02-x0-1>0”的否定是“?x∈R,x2-x-1≤0”,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∧(¬q) | C. | p∨q | D. | p∨(¬q) |
6.A,B为△ABC的内角,A>B是sinA>sinB的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
16.据如图的流程图可得结果为( )
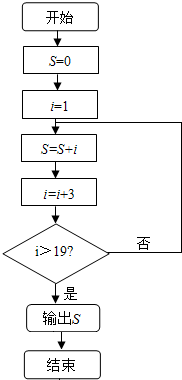

| A. | 19 | B. | 67 | C. | 51 | D. | 70 |
3.a,b,c为△ABC三边之长,若(a+b+c)(a+b-c)=ab,则△ABC的最大角为( )
| A. | 30° | B. | 120° | C. | 90° | D. | 60° |
1.下列推理中属于归纳推理且结论正确的是( )
| A. | 设数列﹛an﹜的前n项和为sn,由an=2n-1,求出s1=12,s2=22,s3=32,…推断sn=n2 | |
| B. | 由f(x)=xcosx,满足f(-x)=-f(x)对?x∈R都成立,推断f(x)=xcosx为奇函数 | |
| C. | 由圆x2+y2=r2的面积s=πr2推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的面积s=πab | |
| D. | 由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断对一切正整数n,(n+1)2>2n |