Question

14．若实数x，y满足约束条件$\left\{\begin{array}{l}x≥1\\ y≤2\\ x-y-1≤0.\end{array}\right.$
（1）求该不等式组表示的平面区域的面积；
（2）求z=x+y的最大值．

Answer 1

分析 （1）作出不等式组对应的平面区域求出对应交点的坐标即可求该不等式组表示的平面区域的面积；
（2）利用目标函数z=x+y的几何意义，利用平移法即可求z的最大值．

解答 解：（1）作出线性约束条件所表示的平面区域如图所示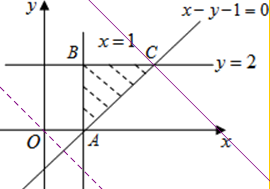，…（3分）
∵A（1，0），B（1，2），C（3，2），…（4分）
∴$平面区域的面积是\frac{1}{2}×2×2=2$；…（6分）
（2）作直线x+y=0并平移至点C（3，2）时，z有最大值，
即当x=3，y=2时，z_max=3+2=5．…（12分）

点评 本题主要考查线性规划的应用，根据目标函数的几何意义，利用数形结合是解决本题的关键．