题目内容

14．若关于x的方程sin2x+sinx-1+m=0有解，则实数m的取值范围为[-1，$\frac{5}{4}$]．

分析 由题意可得m=-sin2x-sinx+1=-${（sinx+\frac{1}{2}）}^{2}$+$\frac{5}{4}$，再利用二次函数的性质求得m的范围．

解答 解：关于x的方程sin2x+sinx-1+m=0有解，即 m=-sin2x-sinx+1=-${（sinx+\frac{1}{2}）}^{2}$+$\frac{5}{4}$，
故当sinx=-$\frac{1}{2}$时，m取得最大值为$\frac{5}{4}$；当sinx=1时，m取得最小值为-1，
故实数m的取值范围为[-1，$\frac{5}{4}$]，
故答案为：[-1，$\frac{5}{4}$]．

点评 本题主要考查二次函数的性质，正弦函数的值域，属于基础题．

练习册系列答案
相关题目
4．已知顶点在原点O，准线方程是y=-1的抛物线与过点M（0，1）的直线l交于A，B两点，若直线OA和直线OB的斜率之和为1
（Ⅰ）求此抛物线的标准方程；
（Ⅱ）求直线l的方程．
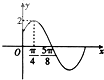5．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）求方程f（$\frac{3x}{4}$-$\frac{π}{8}$）=f（$\frac{π}{2}$）的解．
2．满足$\sqrt{3}z+iz=4（\sqrt{3}-i）$的复数z的共轭复数$\overline z$=2+2$\sqrt{3}$i．
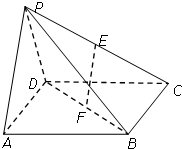9．如图，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD，且PA=PD=$\frac{{\sqrt{2}}}{2}$a．
（1）求证：EF∥平面PAD；
（2）求三棱锥E-PBD的体积．
19．已知x2-y2+2xyi=2i，求实数x、y的值．
6．E、F分别是边长为1的正方形ABCD边BC、CD的中点，沿线AF，AE，EF折起来，则所围成的三棱锥的体积为（　　）
A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{1}{12}$D．$\frac{1}{24}$
3．已知函数$f（x）=sin（2ωx+\frac{π}{6}）$，其最小正周期为$\frac{π}{2}$．
（1）求f（x）的表达式；
（2）将函数f（x）的图象向右平移$\frac{π}{8}$个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数y=g（x）的图象，若关于x的方程g（x）+k=0，在区间$[{0，\frac{π}{2}}]$上有且只有一个实数解，求实数k的取值范围．
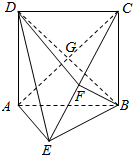4．如图，矩形ABCD中，BC⊥平面ABE，且BC=4，AE=EB，F为CE的中点，且BF⊥平面ACE，B∩AC=G  
（1）求证：AE∥平面BFD；
（2）求证：AE⊥平面BCE；
（3）求三棱锥E-ADC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网