题目内容
5.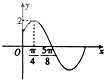 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)求方程f($\frac{3x}{4}$-$\frac{π}{8}$)=f($\frac{π}{2}$)的解.
分析 (1)由函数图象可得A,T,利用周期公式可解得ω,又由f($\frac{π}{4}$)=2sin($\frac{4}{3}$×$\frac{π}{4}$+φ)=2,结合范围|φ|<$\frac{π}{2}$,可解得φ,从而可求函数f(x)的解析式.
(2)由(1)可得f($\frac{3x}{4}$-$\frac{π}{8}$)=2sinx,f($\frac{π}{2}$)=1,所以原方程可化为2sinx=1,利用正弦函数的图象和性质即可得解.
解答 解:(1)由函数图象可得:A=2,T=$\frac{2π}{ω}=(\frac{5π}{8}-\frac{π}{4})×4$,解得:$ω=\frac{4}{3}$,
所以:f(x)=2sin($\frac{4}{3}$x+φ),又f($\frac{π}{4}$)=2sin($\frac{4}{3}$×$\frac{π}{4}$+φ)=2,|φ|<$\frac{π}{2}$,
可解得:φ=$\frac{π}{6}$,
所以函数f(x)的解析式为:f(x)=2sin($\frac{4}{3}$x+$\frac{π}{6}$)…6分
(2)由(1)可得f($\frac{3x}{4}$-$\frac{π}{8}$)=2sin[($\frac{4}{3}$($\frac{3x}{4}$-$\frac{π}{8}$)+$\frac{π}{6}$]=2sinx,
f($\frac{π}{2}$)=2sin($\frac{4}{3}$×$\frac{π}{2}$+$\frac{π}{6}$)=2sin$\frac{5π}{6}$=1,
所以方程f($\frac{3x}{4}$-$\frac{π}{8}$)=f($\frac{π}{2}$)可化为:2sinx=1,即sinx=$\frac{1}{2}$,
解得:x=2k$π+\frac{π}{6}$或x=2k$π+\frac{5π}{6}$,k∈Z…12分
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,属于基本知识的考查.

| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 相交且过圆心 |
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |