题目内容
7．设{an}为递减的等比数列，其中q为公比，前n项和Sn，且{a1，a2，a3}⊆{-4，-3，-2，0，1，2，3，4}，则$\frac{S_8}{{1-{q^4}}}$=$\frac{17}{2}$．分析 根据递减的等比数列特征求出a1、a2、a3的值，即可求出公比，利用等比数列的前n项和公式求出式子的值．
解答 解：由题意可得，a1=4，a2=2，a3=1，
所以公比q=$\frac{1}{2}$，
则$\frac{{S}_{8}}{1-{q}^{4}}$=$\frac{\frac{4（1-{q}^{8}）}{1-q}}{1-{q}^{4}}$=$\frac{4（1+{q}^{4}）}{1-q}$=4（1+$\frac{1}{16}$）×2=$\frac{17}{2}$，
故答案为：$\frac{17}{2}$．
点评 本题考查递减等比数列的性质，以及等比数列的前n项和公式，属于中档题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
17．已知命题p：?x0∈R，sinx0=$\sqrt{2}$；命题q：?x∈R，x2-x+1＞0．则下列结论正确的是（ ）
| A． | 命题是p∨q假命题 | B． | 命题是p∧q真命题 | ||
| C． | 命题是（?p）∨（?q）真命题 | D． | 命题是（?p）∧（?q）真命题 |
18．要得到函数f（x）=sin（2x+$\frac{π}{4}$）的图象，只需将函数g（x）=sin2x的图象（ ）
| A． | 向左平移$\frac{π}{8}$个单位长度 | B． | 向右平移$\frac{π}{8}$个单位长度 | ||
| C． | 向左平移$\frac{π}{4}$个单位长度 | D． | 向右平移$\frac{π}{4}$个单位长度 |
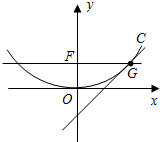设p＞0，抛物线方程为C：x2=2px．如图所示，过焦点F作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过点（0，-1）．
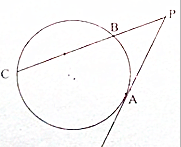如图，PA是圆的切线，A为切点，PBC是圆的割线，且PB=$\frac{1}{2}$BC，则$\frac{PA}{PB}$=$\sqrt{3}$．
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的经过中心的弦称为椭圆的一条直径，平行于该直径的所有弦的中点的轨迹为一条直线段，称为该直径的共轭直径．已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1