题目内容
17.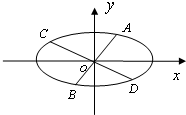 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条直线段,称为该直径的共轭直径.已知椭圆的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1(Ⅰ)若一条直径的斜率为$\frac{1}{2}$,求该直径的共轭直径所在的直线方程;
(Ⅱ)若椭圆的两条共轭直径为AB和CD,它们的斜率分别为k1、k2,证明:四边形ACBD的面积为定值.
分析 (Ⅰ)利用点差法,求该直径的共轭直径所在的直线方程;
(Ⅱ)确定A、B的坐标,C、D的坐标,求出点C到直线AB的距离,可得四边形ACBD的面积,即可得出结论.
解答 (Ⅰ)解:设斜率为$\frac{1}{2}$的直径平行的弦的端点坐标分别为(x1,y1)、(x2,y2),该弦中点为(x,y),
则x1+x2=2x,y1+y1=2y,
(x1,y1)、(x2,y2),代入椭圆方程,相减得:k=$\frac{1}{2}$,
所以得:x+2y=0,
故该直径的共轭直径所在的直线方程为x+2y=0.…(5分)
(Ⅱ)证明:椭圆的两条共轭直径为AB和CD,它们的斜率分别为k1、k2.
四边形ACBD显然为平行四边形,设与AB平行的弦的端点坐标分别为(x1,y1)、(x2,y2),
则${k_1}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$,${k_2}=\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$,故${k_1}{k_2}=\frac{{{y_1}^2-{y_2}^2}}{{{x_1}^2-{x_2}^2}}=-\frac{1}{4}$.
由$\left\{\begin{array}{l}y={k_1}x\\ \frac{x^2}{16}+\frac{y^2}{4}=1\end{array}\right.$得A、B的坐标分别为$(\frac{4}{{\sqrt{1+4k_1^2}}},\frac{{4{k_1}}}{{\sqrt{1+4k_1^2}}})$,$(-\frac{4}{{\sqrt{1+4k_1^2}}},-\frac{{4{k_1}}}{{\sqrt{1+4k_1^2}}})$
故|AB|=$\frac{8}{{\sqrt{1+4k_1^2}}}\sqrt{1+k_1^2}$,
同理C、D的坐标分别为$(\frac{4}{{\sqrt{1+4k_2^2}}},\frac{{4{k_2}}}{{\sqrt{1+4k_2^2}}})$,$(-\frac{4}{{\sqrt{1+4k_2^2}}},-\frac{{4{k_2}}}{{\sqrt{1+4k_2^2}}})$
所以,点C到直线AB的距离$d=\frac{{|{\frac{{4{k_1}}}{{\sqrt{1+4k_2^2}}}-\frac{{4{k_2}}}{{\sqrt{1+4k_2^2}}}}|}}{{\sqrt{1+k_1^2}}}=\frac{{4|{{k_1}-{k_2}}|}}{{\sqrt{1+k_1^2}\sqrt{1+4k_2^2}}}$
设点C到直线AB的距离为d,四边形ACBD的面积为S,
则S=d|AB|=$\frac{{4|{{k_1}-{k_2}}|}}{{\sqrt{1+k_1^2}\sqrt{1+4k_2^2}}}$×$\frac{8}{{\sqrt{1+4k_1^2}}}\sqrt{1+k_1^2}$=$\frac{{32|{{k_1}-{k_2}}|}}{{\sqrt{1+4k_1^2}\sqrt{1+4k_2^2}}}$
=$32\sqrt{\frac{{k_1^2+k_2^2-2{k_1}{k_2}}}{{1+4(k_1^2+k_2^2)+16{k^2}_1{k_2}^2}}}=16$,为定值.…(13分)
点评 本题考查新定义,考查椭圆方程,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | 双曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1与椭圆$\frac{{x}^{2}}{35}$+y2=1有相同的焦点 | |
| B. | “0<x<2”是“x2-2x-3<0”充分不必要条件 | |
| C. | “若xy=0,则x、y中至少有一个为0”的否命题是真命题. | |
| D. | “?x∈R,使x2-2x+3≤0” |
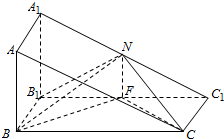 直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.
直三棱柱ABC-A1B1C1中,AB=BB1=$\frac{1}{2}$BC,∠ABC=90°,N、F分别是A1C1、B1C1的中点.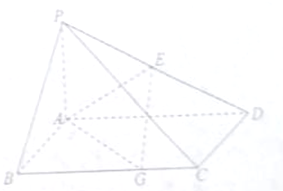 如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.
如图,在四棱锥P-ABCD中,底圆ABCD是矩形,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点,点G在线段BC上,且BG=3.