Question

【题目】已知函数f（x）=x（1﹣a|x|）+1（a＞0），若f（x+a）≤f（x）对任意的x∈R恒成立，则实数a的取值范围是 ．

Answer 1

【答案】[ ，+∞）
【解析】解：∵f（x）=x（1﹣a|x|）+1= = 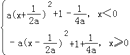（a＞0），
∴f（x+a）=（x+a）（1﹣a|x+a|）+1，
∵f（x+a）≤f（x）对任意的x∈R恒成立，
在同一坐标系中作出满足题意的y=f（x+a）与y=f（x）的图象如下：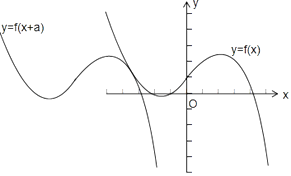

∴x（1+ax）+1≥（x+a）[1﹣a（x+a）]+1恒成立，
即x+ax2+1≥﹣a（x2+2ax+a2）+x+a+1，
整理得：2x2+2ax+a2﹣1≥0恒成立，
∴△=4a2﹣4×2（a2﹣1）≤0，
解得：a≥ ．
所以答案是：[ ，+∞）．