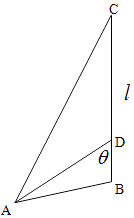题目内容
【题目】如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点
(1)求证:AC 1//平面CDB1;(2)求证:AC⊥面BB1C1C ;

【答案】(1)见解析;(2)见解析.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 中点,连接
中点,连接![]() ,根据中位线可得
,根据中位线可得![]() ∥
∥![]() ,即可证明
,即可证明![]() ∥平面
∥平面![]() ;(2)在直三棱柱
;(2)在直三棱柱![]() 中,结合勾股定理,推出
中,结合勾股定理,推出![]() ,再根据
,再根据![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
(1)证明:连接BC1交CB1于点O,则O为B1C中点.
连接OD,点D是AB的中点,
因此AC1∥OD,
而OD平面B1CD,
AC1不包含于平面B1CD,
∴AC1∥平面CDB1.
(2)证明:直三棱柱ABC-A1B1C1,
底面三边长AC=3,BC=4,AB=5,
∵AC2+BC2=AB2
∴AC⊥BC,
又AC⊥C1C,C1C∩BC=C
∴AC⊥平面BCC1;
∴AC⊥B1C

【题目】一台还可以用的机器由于使用的时间较长,它按不同的转速生产出来的某机械零件有一些会有缺陷,每小时生产有缺陷零件的多少随机器运转的速率而变化,下表为抽样试验结果:
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺陷的零件数y(件) | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果y与x有线性相关的关系,求回归直线方程;
(3)若实际生产中,允许每小时生产的产品中有缺陷的零件最多为10个,那么机器的运转速度应控制在什么范围内?
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个