题目内容
2.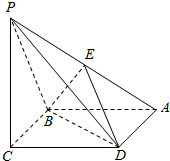 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.(1)求证:平面EBD⊥平面ABCD;
(2)求点E到平面PBC的距离;
(3)求二面角A-BE-D的正切值.
分析 (1)连结AC交BD于点O,连结EO,由三角形中位线定理得EO∥PC.由线面垂直得EO⊥平面ABCD,由此能证明平面EBD⊥平面ABCD.
(2)过O作OF⊥BC于点F,OF为O到平面PBC的距离,OF的长即为E到平面PBC的距离,由此能求出点E到平面PBC的距离.
(3)过O作OH⊥BE于点H,连结AH,∠OHA为所求二面角的平面角,由此能求出二面角A-BE-D的大小.
解答  (1)证明:连结AC交BD于点O,连结EO.
(1)证明:连结AC交BD于点O,连结EO.
∵E、O分别是PA、AC的中点,
∴EO∥PC.又PC⊥平面ABCD,∴EO⊥平面ABCD.
又EO?平面EBD,
∴平面EBD⊥平面ABCD.
(2)解:过O作OF⊥BC于点F,则OF为O到平面PBC的距离.
由于EO∥平面PBC,
∴OF的长即为E到平面PBC的距离,OF=$\frac{\sqrt{3}}{4}$a,
即点E到平面PBC的距离为$\frac{\sqrt{3}}{4}$a.
(3)解:过O作OH⊥BE于点H,连结AH,
则∠OHA为所求二面角的平面角,
在Rt△BOE中,OH=$\frac{OB×OE}{BE}$=$\frac{\frac{a}{2}×\frac{a}{2}}{\frac{\sqrt{2}}{2}a}$=$\frac{\sqrt{2}}{4}a$,OA=$\frac{\sqrt{3}}{2}a$,
∴tan∠OHA=$\frac{OA}{OH}$=$\sqrt{6}$.
故二面角A-BE-D的大小为arctan$\sqrt{6}$.
点评 本题考查面面垂直的证明,考查点到平面的距离的求法,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.在△ABC中,角A,B,C所对的边a,b,c成等比数列,则角B的取值范围是( )
| A. | [$\frac{π}{3}$,π) | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | (0,$\frac{π}{6}$] |
13.实数x,y,z满足x2-2x+y=z-1且x+y2+1=0,则x,y,z满足的下列关系式为( )
| A. | z≥y>x | B. | z≥x>y | C. | x>z≥y | D. | z>x≥y |
7.已知四个函数y=3x,y=x2,y=3x,y=log3x,其中奇函数是( )
| A. | y=3x | B. | y=x2 | C. | y=3x | D. | y=log3x |