题目内容
8.在△ABC中,角A,B,C所对的边a,b,c成等比数列,则角B的取值范围是( )| A. | [$\frac{π}{3}$,π) | B. | [$\frac{π}{6}$,π) | C. | (0,$\frac{π}{3}$] | D. | (0,$\frac{π}{6}$] |
分析 公比为q,则q>0,a=$\frac{b}{q}$,c=bq,由余弦定理得cosB=$\frac{1}{2}$(q2+$\frac{1}{{q}^{2}}$-1)≥$\frac{1}{2}×(2\sqrt{{q}^{2}×\frac{1}{{q}^{2}}}-1)$=$\frac{1}{2}$,由此能求出角B的取值范围.
解答 解:∵在△ABC中,角A,B,C所对的边a,b,c成等比数列,
∴设公比为q,则q>0,a=$\frac{b}{q}$,c=bq,
∴cosB=$\frac{\frac{{b}^{2}}{{q}^{2}}+{b}^{2}{q}^{2}-{b}^{2}}{2×\frac{b}{q}×bq}$=$\frac{1}{2}$(q2+$\frac{1}{{q}^{2}}$-1)≥$\frac{1}{2}×(2\sqrt{{q}^{2}×\frac{1}{{q}^{2}}}-1)$=$\frac{1}{2}$,
∵B是△ABC的内角,∴0$<B<\frac{π}{3}$,
∴角B的取值范围是(0,$\frac{π}{3}$].
故选:C.
点评 本题考查三角形的内角的取值范围的求法,是中档题,解题时要注意等比数列、余弦定理的性质的合理运用.

练习册系列答案
相关题目
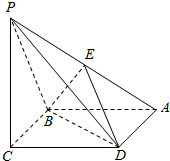 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.