题目内容
14.直线l:x+y-4=0与圆C:x2+y2+2x=0的位置关系为相离.分析 把圆的方程化为标准方程后,找出圆心坐标与圆的半径r,然后利用点到直线的距离公式求出圆心到已知直线的距离d,然后比较d与r的大小即可得到直线与圆的位置关系,然后把圆心坐标代入已知直线即可判断已知直线是否过圆心.
解答 解:由圆C:x2+y2+2x=0化为标准方程得:(x+1)2+y2=1,
所以圆心坐标为(-1,0),圆的半径r=1,
则圆心到直线x+y-4=0的距离d=$\frac{5}{\sqrt{2}}$>r=1,所以直线与圆相离,
故答案为:相离.
点评 此题考查学生掌握判断直线与圆位置关系的方法,灵活运用点到直线的距离公式化简求值,是一道综合题.

练习册系列答案
相关题目
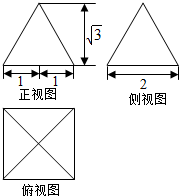
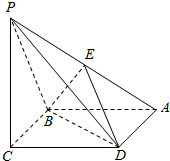 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.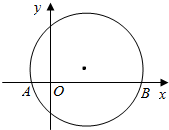 已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.
已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.