题目内容
9.已知函数f(x)=log2${\;}^{(a{x}^{2}-2x+2)}$(1)若f(x)的定义域为实数集R,求实数a的取值范围,并求此时f(x)的值域.
(2)若方程log2${\;}^{(a{x}^{2}-2x+2)}$=2在[$\frac{1}{2}$,2]内有解,求实数a的取值范围.
分析 (1)由题意得ax2-2x+2>0对于任意的实数都成立,验证a=0是否成立,a≠0时根据二次函数的图象找出等价条件,求出a的范围.
(2)求参数一般转化为求最值.求出解析式对应函数的值域,让该参数是该值域的一个元素即可保证存在性
解答 解:(1)∵函数y=log2(ax2-2x+2)的定义域为R,∴ax2-2x+2>0对于任意的实数都成立;
当a=0时,-2x+2>0,故不符合题意;
当a≠0时,则有$\left\{\begin{array}{l}{a>0}\\{4-8a<0}\end{array}\right.$,解得a>$\frac{1}{2}$,此时f(x)的值域是(log2(2-$\frac{1}{a}$),+∞);
(2)∵方程log2${\;}^{(a{x}^{2}-2x+2)}$=2在[$\frac{1}{2}$,2]内有解,
∴ax2-2x-2=0在[$\frac{1}{2}$,2]内有解,
∴a=$\frac{2}{x}+\frac{2}{{x}^{2}}$=$2(\frac{1}{x}+\frac{1}{2})^{2}$-$\frac{1}{2}$在[$\frac{1}{2}$,2]内成立.
∵$\frac{3}{2}$≤$2(\frac{1}{x}+\frac{1}{2})^{2}$-$\frac{1}{2}$≤12,
∴$\frac{3}{2}$≤a≤12,
∴实数a的取值范围是[$\frac{3}{2}$,12].
点评 本题的考点是对数函数的定义域和二次函数恒成立问题,注意验证特殊情况,结合二次函数的图象找出等价条件.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
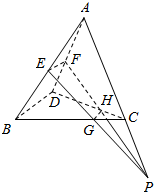 已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
已知空间四边形ABCD中,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且$\frac{BG}{GC}=\frac{DH}{HC}$=2,求证:直线EG,FH,AC相交于同一点P.
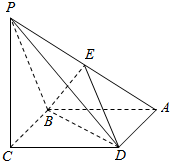 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.