题目内容
(本小题满分12分)
已知数列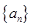 的前
的前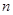 项和为
项和为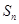 ,函数
,函数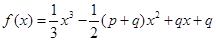 ,
,
(其中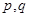 均为常数,且
均为常数,且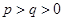 ),当
),当 时,函数
时,函数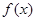 取得极小值.
取得极小值.
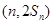
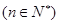 均在函数
均在函数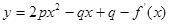 的图像上(其中
的图像上(其中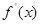 是
是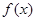 的导函数).
的导函数).
(Ⅰ)求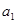 的值;
的值;
(Ⅱ)求数列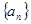 的通项公式.
的通项公式.
已知数列
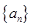 的前
的前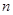 项和为
项和为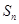 ,函数
,函数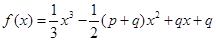 ,
,(其中
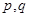 均为常数,且
均为常数,且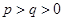 ),当
),当 时,函数
时,函数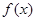 取得极小值.
取得极小值.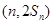
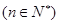 均在函数
均在函数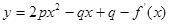 的图像上(其中
的图像上(其中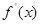 是
是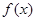 的导函数).
的导函数).(Ⅰ)求
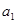 的值;
的值;(Ⅱ)求数列
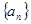 的通项公式.
的通项公式.(Ⅰ)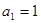 (Ⅱ)
(Ⅱ)
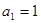 (Ⅱ)
(Ⅱ)
试题分析:(Ⅰ)因为
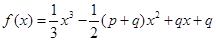 ,
,所以
 .
.令
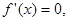 得
得 ,或
,或 .
.由此可得下表
| |  | 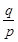 | 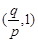 |  | 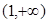 |
 | + | 0 | - | 0 | + |
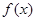 | 增 | 极大值 | 减 | 极小值 | 增 |
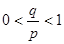 ,所以
,所以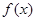 在
在 处取得唯一的极小值,可得
处取得唯一的极小值,可得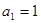 . ……6分
. ……6分(Ⅱ)由题意知函数
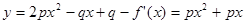 ,
,因为
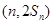 均在函数
均在函数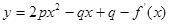 的图像上,
的图像上,所以

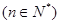 .
.由于
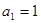 ,所以
,所以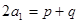 ,得
,得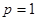 , ……8分即
, ……8分即  ①
①当
 时,
时,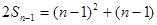 ②
②①-② ,得
 时,
时,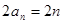
所以

已知
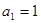 也满足上述公式,故数列的通项公式为
也满足上述公式,故数列的通项公式为 . ……12分
. ……12分 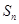 求
求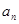 ,考查了学生综合运用所学知识解决问题的能力和运算求解能力.
,考查了学生综合运用所学知识解决问题的能力和运算求解能力.点评:利用导数求极值或最值时,画表格比较清楚直观,已知
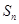 求
求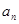 要分
要分 和
和 两种情况,而且不要忘记验证
两种情况,而且不要忘记验证 时的
时的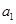 是否适合
是否适合 时求出的
时求出的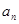 .
.
练习册系列答案
相关题目
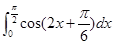 ,则二项式(x2+
,则二项式(x2+ )5的展开式中x的系数为 .
)5的展开式中x的系数为 .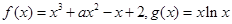
 的单调递减区间为
的单调递减区间为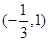 ,求函数
,求函数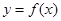 的图像过点
的图像过点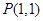 的切线方程;
的切线方程;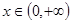 ,
, 恒成立,求实数
恒成立,求实数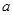 的取值范围.
的取值范围. 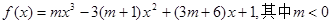 。
。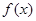 的单调增区间是(0,1)求m的值。
的单调增区间是(0,1)求m的值。 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于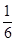
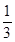
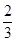
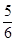
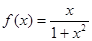 ,则
,则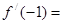

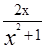 - 2的极值.
- 2的极值.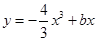 有三个单调区间,则
有三个单调区间,则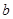 的取值范围是 .
的取值范围是 . 的最小值是______.
的最小值是______.