题目内容
已知a>b>1,c<0,给出下列四个结论:
① >
> ;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
其中所有正确结论的序号是( )
①
 >
> ;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.其中所有正确结论的序号是( )
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
A
a>b>1⇒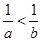 ,
,
又c<0,故 >
> ,故①正确;
,故①正确;
由c<0知,y=xc在(0,+∞)上是减函数,故ac<bc.故②正确.
由已知得a-c>b-c>1.
故logb(a-c)>logb(b-c).
由a>b>1得0<loga(b-c)<logb(b-c),
故logb(a-c)>loga(b-c).故③正确.
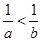 ,
,又c<0,故
 >
> ,故①正确;
,故①正确;由c<0知,y=xc在(0,+∞)上是减函数,故ac<bc.故②正确.
由已知得a-c>b-c>1.
故logb(a-c)>logb(b-c).
由a>b>1得0<loga(b-c)<logb(b-c),
故logb(a-c)>loga(b-c).故③正确.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 ,
, =
= ,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=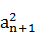 -
-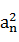 (n≥1,n∈N+).
(n≥1,n∈N+). ,则下列关系中正确的是( )
,则下列关系中正确的是( )



 ,
, )时, f(x)≤g(x),求a的取值范围.
)时, f(x)≤g(x),求a的取值范围. 是定义在
是定义在 上的函数,若
上的函数,若 ,且对任意
,且对任意 ,满足
,满足 ,
, ,则
,则 =( )
=( )
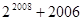


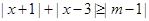 恒成立,则
恒成立,则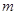 的取值范围为 .
的取值范围为 . <0的解集为( )
<0的解集为( )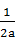 +
+ ,B=
,B= (a>0,b>0),则A,B的大小关系为 .
(a>0,b>0),则A,B的大小关系为 .