题目内容
已知数列{an}满足:a1= ,
,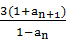 =
=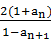 ,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=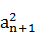 -
-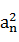 (n≥1,n∈N+).
(n≥1,n∈N+).
(1)求数列{an},{bn}的通项公式.
(2)证明:数列{bn}中的任意三项不可能成等差数列.
 ,
,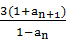 =
=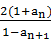 ,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=
,anan+1<0(n≥1,n∈N+),数列{bn}满足:bn=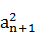 -
-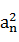 (n≥1,n∈N+).
(n≥1,n∈N+).(1)求数列{an},{bn}的通项公式.
(2)证明:数列{bn}中的任意三项不可能成等差数列.
(1)an=(-1)n-1·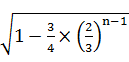 bn=
bn= ×
× (2)见解析
(2)见解析
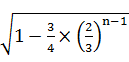 bn=
bn= ×
× (2)见解析
(2)见解析(1)由题意知,1-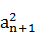 =
= (1-
(1-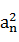 ),
),
令Cn=1-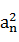 ,则Cn+1=
,则Cn+1= Cn,又C1=1-
Cn,又C1=1- =
= ,
,
则数列{Cn}是首项为C1= ,公比为
,公比为 的等比数列,即Cn=
的等比数列,即Cn= ×
× ,
,
故1-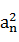 =
= ×
× ⇒
⇒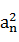 =1-
=1- ×
× ,
,
又a1= >0,anan+1<0,
>0,anan+1<0,
故an=(-1)n-1·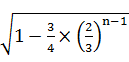 ,
,
bn=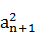 -
-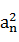
= -
-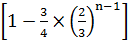
= ×
× .
.
(2)假设数列{bn}中存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,由于数列{bn}是首项为 ,公比为
,公比为 的等比数列,于是有br>bs>bt,则只可能有2bs=br+bt成立.
的等比数列,于是有br>bs>bt,则只可能有2bs=br+bt成立.
所以2× =
= +
+ ,
,
两边同乘3t-1·21-r化简得2×2s-r·3t-s=3t-r+2t-r,
由于r<s<t,所以上式右边为奇数,左边为偶数,故上式不可能成立,导致矛盾,
故数列{bn}中任意三项不可能成等差数列.
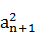 =
= (1-
(1-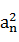 ),
),令Cn=1-
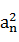 ,则Cn+1=
,则Cn+1= Cn,又C1=1-
Cn,又C1=1- =
= ,
,则数列{Cn}是首项为C1=
 ,公比为
,公比为 的等比数列,即Cn=
的等比数列,即Cn= ×
× ,
,故1-
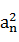 =
= ×
× ⇒
⇒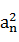 =1-
=1- ×
× ,
,又a1=
 >0,anan+1<0,
>0,anan+1<0,故an=(-1)n-1·
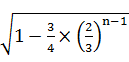 ,
,bn=
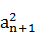 -
-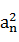
=
 -
-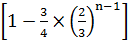
=
 ×
× .
.(2)假设数列{bn}中存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,由于数列{bn}是首项为
 ,公比为
,公比为 的等比数列,于是有br>bs>bt,则只可能有2bs=br+bt成立.
的等比数列,于是有br>bs>bt,则只可能有2bs=br+bt成立.所以2×
 =
= +
+ ,
,两边同乘3t-1·21-r化简得2×2s-r·3t-s=3t-r+2t-r,
由于r<s<t,所以上式右边为奇数,左边为偶数,故上式不可能成立,导致矛盾,
故数列{bn}中任意三项不可能成等差数列.

练习册系列答案
相关题目
 2|x-3|+|x-4|.
2|x-3|+|x-4|. 的解集;
的解集; 的解集不是空集,求实数a的取值范围.
的解集不是空集,求实数a的取值范围. >
> ;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c. 和
和 的解集分别为
的解集分别为 和
和 ,那么称这两个不等式为对偶不等式. 如果不等式
,那么称这两个不等式为对偶不等式. 如果不等式 与不等式
与不等式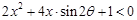 为对偶不等式,且
为对偶不等式,且 ,则
,则 .
. 表示的曲线是( )
表示的曲线是( )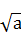 +b
+b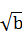 >a
>a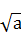 +
+ +
+ 的最大值为 .
的最大值为 .
