题目内容
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1,且当x∈[- ,
, )时, f(x)≤g(x),求a的取值范围.
)时, f(x)≤g(x),求a的取值范围.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1,且当x∈[-
 ,
, )时, f(x)≤g(x),求a的取值范围.
)时, f(x)≤g(x),求a的取值范围.(1){x|0<x<2}
(2)(-1, ]
]
(2)(-1,
 ]
](1)当a=-2时,不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.
设函数y=|2x-1|+|2x-2|-x-3,则
y= ,其图象如图所示.
,其图象如图所示.

从图象可知,当且仅当x∈(0,2)时,y<0.所以原不等式的解集是{x|0<x<2}.
(2)当x∈[- ,
, )时, f(x)=1+a.
)时, f(x)=1+a.
不等式f(x)≤g(x)化为1+a≤x+3.
所以x≥a-2对x∈[- ,
, )都成立.
)都成立.
故- ≥a-2,即a≤
≥a-2,即a≤ .
.
从而a的取值范围是(-1, ]
]
设函数y=|2x-1|+|2x-2|-x-3,则
y=
 ,其图象如图所示.
,其图象如图所示.
从图象可知,当且仅当x∈(0,2)时,y<0.所以原不等式的解集是{x|0<x<2}.
(2)当x∈[-
 ,
, )时, f(x)=1+a.
)时, f(x)=1+a.不等式f(x)≤g(x)化为1+a≤x+3.
所以x≥a-2对x∈[-
 ,
, )都成立.
)都成立.故-
 ≥a-2,即a≤
≥a-2,即a≤ .
.从而a的取值范围是(-1,
 ]
]
练习册系列答案
相关题目
 +
+ ≥
≥

 2|x-3|+|x-4|.
2|x-3|+|x-4|. 的解集;
的解集; 的解集不是空集,求实数a的取值范围.
的解集不是空集,求实数a的取值范围. >
> ;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c. 和
和 的解集分别为
的解集分别为 和
和 ,那么称这两个不等式为对偶不等式. 如果不等式
,那么称这两个不等式为对偶不等式. 如果不等式 与不等式
与不等式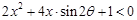 为对偶不等式,且
为对偶不等式,且 ,则
,则 .
.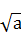 +
+ +
+ 的最大值为 .
的最大值为 . 的解集为___________.
的解集为___________.