题目内容
【题目】已知圆C:x2+y2﹣2x+4my+4m2=0,圆C1:x2+y2=25,以及直线l:3x﹣4y﹣15=0.
(1)求圆C1:x2+y2=25被直线l截得的弦长;
(2)当m为何值时,圆C与圆C1的公共弦平行于直线l;
(3)是否存在m,使得圆C被直线l所截的弦AB中点到点P(2,0)距离等于弦AB长度的一半?若存在,求圆C的方程;若不存在,请说明理由.
【答案】解:(1)因为圆![]() 的圆心O(0,0),半径r=5,
的圆心O(0,0),半径r=5,
所以,圆心O到直线l:3x﹣4y﹣15=0的距离d:![]() ,由勾股定理可知,
,由勾股定理可知,
圆![]() 被直线l截得的弦长为
被直线l截得的弦长为![]() .
.
(2)圆C与圆C1的公共弦方程为2x﹣4my﹣4m2﹣25=0,
因为该公共弦平行于直线3x﹣4y﹣15=0,
则![]() ≠
≠![]() ,
,
解得:m=![]()
经检验m=![]() 符合题意,故所求m=
符合题意,故所求m=![]() ;
;
(3)假设这样实数m存在.
设弦AB中点为M,由已知得|AB|=2|PM|,即|AM|=|BM|=|PM|
所以点P(2,0)在以弦AB为直径的圆上.
设以弦AB为直径的圆方程为:x2+y2﹣2x+4my+4m2+λ(3x﹣4y﹣15)=0,
则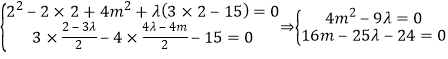
消去λ得:100m2﹣144m+216=0,25m2﹣36m+54=0
因为△=362﹣4×25×54=36(36﹣25×6)<0
所以方程25m2﹣36m+54=0无实数根,
所以,假设不成立,即这样的圆不存在.
【解析】(1)根据直线和圆相交的弦长公式即可求圆C1:x2+y2=25被直线l截得的弦长;
(2)求出两圆的公共弦结合直线平行的条件即可求出直线l;
(3)根据两点间的距离公式结合弦长关系即可得到结论.

练习册系列答案
相关题目