题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),
),![]() 为
为![]() 上一点,以
上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三点按逆时针方向排列.
三点按逆时针方向排列.
(Ⅰ)当点![]() 在
在![]() 上运动时,求点
上运动时,求点![]() 运动轨迹的直角坐标方程;
运动轨迹的直角坐标方程;
(Ⅱ)若曲线![]() :
: ![]() ,经过伸缩变换
,经过伸缩变换![]() 得到曲线
得到曲线![]() ,试判断点
,试判断点![]() 的轨迹与曲线
的轨迹与曲线![]() 是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
是否有交点,如果有,请求出交点的直角坐标,没有则说明理由.
【答案】(1)![]() (2)
(2)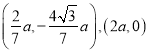 .
.
【解析】试题分析:考虑到![]() 则
则![]() 点的极坐标可以表示为
点的极坐标可以表示为![]() 将
将![]() 点代入直线
点代入直线![]() 的极坐标方程中得到关于
的极坐标方程中得到关于![]() 的方程即为
的方程即为![]() 点的极坐标方程,再转化为
点的极坐标方程,再转化为![]() 点的直角坐标方程.(2)将曲线
点的直角坐标方程.(2)将曲线![]() 的普通方程与直线
的普通方程与直线![]() 普通方程联立
普通方程联立![]() 故必有两个交点.
故必有两个交点.
试题解析:(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,
,
则由题意可得点![]() 的坐标为
的坐标为![]() ,
,
再由点![]() 的横坐标等于
的横坐标等于![]() ,
, ![]() ,
,
可得![]() ,
,
可得![]() ,
,
故当点![]() 在
在![]() 上运动时点
上运动时点![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)曲线![]() :
: ![]() ,
,
![]() ,即
,即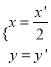 ,代入
,代入![]() ,即
,即![]() ,
,
联立点![]() 的轨迹方程,消去
的轨迹方程,消去![]() 得
得![]() ,
,
![]() 有交点,坐标分别为
有交点,坐标分别为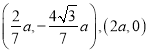 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目