Question

【题目】已知函数f（x）=
（1）证明f（x）是奇函数；
（2）判断f（x）的单调性，并用定义证明
（3）求f（x）在[1，2]上的最值．

Answer 1

【答案】解：（1）由于函数f（x）=的定义域为R，f（﹣x）===﹣f（x），
故函数f（x）为奇函数．
（2）由于f（x）===1﹣，设x1＜x2 ， 则＜，
根据f（x1）﹣f（x2）=[1﹣]﹣[1﹣]=﹣
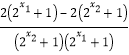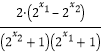==＜0，∴f（x1）＜f（x2），
故函数f（x）在R上为增函数．
（3）在[1，2]上，函数f（x）为增函数，故当x=1时，函数f（x）取得最小值为，
当x=2时，函数f（x）取得最大值为．
【解析】（1）由条件利用奇函数的定义进行判断，可得结论．
（2）由条件利用函数的单调性的定义进行证明，可得结论．
（3）由条件利用函数的单调性求得f（x）在[1，2]上的最值．
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识，掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性，以及对三角函数的最值的理解，了解函数，当时，取得最小值为；当时，取得最大值为，则，，．