题目内容
在棱长为1的正方体ABCD-A B
B C
C D
D 的底面A
的底面A B
B C
C D
D 内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为( )
内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为( )
 A.
A.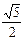 B.
B.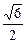 C.
C.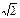 D.
D.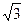
 B
B C
C D
D 的底面A
的底面A B
B C
C D
D 内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为( )
内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为( ) A.
A.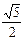 B.
B.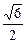 C.
C.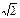 D.
D.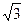
C
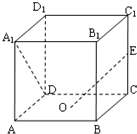
由∠EAB=∠EAD,则E点必在A1C 上,
上,
且E 在面A1C上的射影在AC上为F, 如图, ∵cos∠FAM=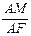 =
=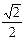 ,
,
∴cos∠BAE=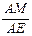 =
=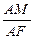 ·
·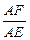 =cos60°=
=cos60°=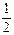 , ∴cos∠FAE= cos∠AEA
, ∴cos∠FAE= cos∠AEA =
=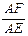 =
=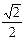 ,则∠AEA
,则∠AEA =45°,
=45°,
∴△AEA 为等腰直角三角形,故AE=
为等腰直角三角形,故AE=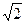 。
。
 上,
上,且E 在面A1C上的射影在AC上为F, 如图, ∵cos∠FAM=
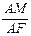 =
=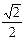 ,
, ∴cos∠BAE=
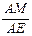 =
=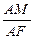 ·
·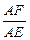 =cos60°=
=cos60°=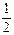 , ∴cos∠FAE= cos∠AEA
, ∴cos∠FAE= cos∠AEA =
=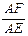 =
=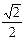 ,则∠AEA
,则∠AEA =45°,
=45°,∴△AEA
 为等腰直角三角形,故AE=
为等腰直角三角形,故AE=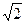 。
。
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

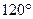 ,则AD与平面BCD所成的角为( )
,则AD与平面BCD所成的角为( )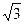 ,用
,用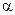 表示∠ASD,求
表示∠ASD,求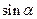
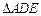 沿DE折起,使二面角
沿DE折起,使二面角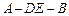 的大小为
的大小为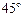 ,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小为 .
,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小为 .