题目内容
【题目】如图，⊙O是△ABC的外接圆，D是 
的中点，BD交AC于E． （Ⅰ）求证：DC2=DEDB；
（Ⅱ）若CD=2 
，O到AC的距离为1，求⊙O的半径r．
【答案】（I）证明：连接OD，OC，由已知D是弧AC的中点，可得∠ABD=∠CBD ∵∠ABD=∠ECD
∴∠CBD=∠ECD
∵∠BDC=∠EDC
∴△BCD∽△CED
∴ 
∴CD2=DEDB．
（II）解：设⊙O的半径为R
∵D是弧AC的中点
∴OD⊥AC，设垂足为F
在直角△CFO中，OF=1，OC=R，CF= 
在直角△CFD中，DC2=CF2+DF2
∴ 
∴R2﹣R﹣6=0
∴（R﹣3）（R+2）=0
∴R=3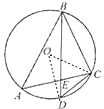
【解析】（I）先证明△BCD∽△CED，可得 
，从而问题得证；（II）OD⊥AC，设垂足为F，求出CF= 
，利用DC2=CF2+DF2 ， 建立方程，即可求得⊙O的半径．
练习册系列答案
相关题目
