Question

【题目】已知圆经过两点，且圆心在直线l：上．

Ⅰ求圆的方程；

Ⅱ求过点且与圆相切的直线方程；

Ⅲ设圆与x轴相交于A、B两点，点P为圆上不同于A、B的任意一点，直线PA、PB交y轴于M、N点当点P变化时，以MN为直径的圆是否经过圆内一定点？请证明你的结论．

Answer 1

【答案】（Ⅰ）；（Ⅱ）或；（Ⅲ）经过定点．

【解析】

Ⅰ设圆圆心为，由求得a的值，可得圆心坐标和半径，从而求得圆的标准方程．

Ⅱ当切线斜率不存在时，求得的方程；当切线斜率存在时，设切线：，由圆心到切线的距离等于半径求得k的值，可得切线的方程．

Ⅲ设，由条件求得M、N的坐标，可得圆的方程再根据定点在x轴上，求出定点的坐标．

解：Ⅰ法一：设圆圆心为，由得，，

解得，，半径为，

所以圆：．

Ⅱ当切线斜率不存在时，：．

当切线斜率存在时，设切线：，

即，由圆心到切线的距离，

解得，此时：．

综上：：或

Ⅲ设，则．

又，，

所以：，，：，

圆的方程为．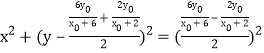

化简得．

由动点关于x轴的对称性可知，定点必在x轴上，令，得．

又点在圆内，

所以当点P变化时，以MN为直径的圆经过定点．