题目内容
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
C
解析试题分析:A.  是偶函数,但在
是偶函数,但在 上单调递减的;
上单调递减的;
B.  是奇函数;
是奇函数;
C. 根据指数函数的图像和函数图像的变换画出函数 的图像,由图像可知满足题意;
的图像,由图像可知满足题意;
D.  的定义域为
的定义域为 ,所以是非奇非偶函数。
,所以是非奇非偶函数。
因此只有C满足题意。
考点:函数的奇偶性;函数的单调性;幂函数的性质;图像的变换。
点评:熟练掌握基本初等函数的图像及性质是解决本题的前提条件。判断函数的奇偶性有两步:一求函数的定义域,看定义域是否关于原点对称;二判断 与
与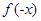 的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。
的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。

练习册系列答案
相关题目
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
设函数 的定义域为
的定义域为 ,
,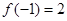 ,对于任意的
,对于任意的 ,
, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B. | C. | D. |
设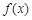 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则
| A.-1 | B.-3 | C.1 | D.3 |
已知函数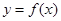 的周期为2,当
的周期为2,当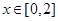 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
下列四个函数:(1) (2)
(2) (3)
(3)
(4) ,其中同时满足:①
,其中同时满足:① ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量 ,都有
,都有 的函数个数为
的函数个数为
| A.1 | B.2 | C.3 | D.4 |
已知函数 的零点分别为
的零点分别为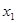 ,
, ,则( )
,则( )
A. | B. |
C. | D. |
下列函数中,在其定义域内既是减函数又是奇函数为( )
A.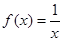 | B. |
C. | D. |