题目内容
设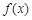 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则
| A.-1 | B.-3 | C.1 | D.3 |
B
解析试题分析:求解函数值,利用奇函数的对称轴,将f(1)=-f(-1),然后根据当x≤0时,f(x)=2x2-x,
∴f(-1)=2(-1)2-(-1)=3,
又∵f(x)是定义在R上的奇函数
∴f(1)=-f(-1)=-3
故选A
考点:本试题主要是考查了函数的奇偶性的运用。
点评:解决这类奇偶性问题的思路,就是利用变量的对称性,将-x的函数值与x的函数值对应起来。熟练掌握函数的奇偶性的性质是解答本题的关键,,属于基础题。

练习册系列答案
相关题目
设 用二分法求方程
用二分法求方程 在区间(1,2)上近似解的过程中,计算得到
在区间(1,2)上近似解的过程中,计算得到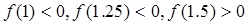 ,则方程的根落在区( )
,则方程的根落在区( )
| A.(1,1.25) | B.(1.25,1.5) | C.(1.5, 1.75) | D.(1.75,2) |
已知定义在R上的奇函数 和偶函数
和偶函数 满足
满足
 ,若
,若 ,则
,则
A. | B. | C. | D.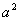 |
下列函数中,既是偶函数又在区间 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
在区间 上不是增函数的是( )
上不是增函数的是( )
A. | B. | C. | D. |
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B.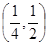 | C.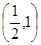 | D.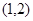 |
 ,函数
,函数 与
与 的图像可能是( )
的图像可能是( )
 的图象如图1所示 , 则其导函数
的图象如图1所示 , 则其导函数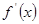 的图象大致形状是( )
的图象大致形状是( ) 