题目内容
设函数 的定义域为
的定义域为 ,
,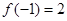 ,对于任意的
,对于任意的 ,
, ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
B
解析试题分析:令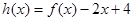 ,则h(-1)=f(-1)-(-2+4)=0,又∵
,则h(-1)=f(-1)-(-2+4)=0,又∵ ,∴
,∴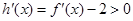 ,∴h(x)在
,∴h(x)在 上是增函数,∴
上是增函数,∴ 可化为h(x)>0,即h(x)>h(-1),利用单调性可知x>-1,故选B
可化为h(x)>0,即h(x)>h(-1),利用单调性可知x>-1,故选B
考点:本题考查了导函数的运用
点评:构造函数,然后利用函数的单调性把抽象函数的解集问题转化为函数的大小比较问题解决

练习册系列答案
相关题目
函数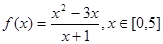 的值域是( )
的值域是( )
| A.[0,2] | B.[0,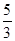 ] ] | C.[-1,2] | D.[-1,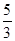 ] ] |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
已知定义在R上的奇函数 和偶函数
和偶函数 满足
满足
 ,若
,若 ,则
,则
A. | B. | C. | D.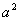 |
下列函数中,既是偶函数又在区间 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
若函数 在
在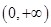 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
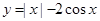 的图象大致是
的图象大致是 
 与
与 (
( 且
且 )的图象可能是( )
)的图象可能是( )



