题目内容
下列四个函数:(1) (2)
(2) (3)
(3)
(4) ,其中同时满足:①
,其中同时满足:① ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量 ,都有
,都有 的函数个数为
的函数个数为
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:① 中
中 ,函数
,函数 是奇函数②对定义域内的任意两个自变量
是奇函数②对定义域内的任意两个自变量 ,都有
,都有 则函数
则函数 是增函数(1)
是增函数(1) 是奇函数,定义域上不是增函数,
是奇函数,定义域上不是增函数,
(2) 既是奇函数又是增函数(3)
既是奇函数又是增函数(3) 是既是奇函数又是减函数(4)
是既是奇函数又是减函数(4) 既是奇函数又是增函数。满足题干的有(2) (4)两个
既是奇函数又是增函数。满足题干的有(2) (4)两个
考点:函数性质奇偶性单调性
点评:若函数满足 则函数为奇函数,若满足
则函数为奇函数,若满足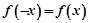 则函数为偶函数,若有
则函数为偶函数,若有 则函数为增函数,若
则函数为增函数,若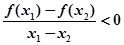 则函数为减函数
则函数为减函数

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列函数中,既是偶函数又在区间 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B.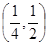 | C.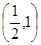 | D.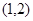 |
若 是偶函数,它在
是偶函数,它在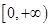 上是减函数,且
上是减函数,且 ,则x的取值范围是( )
,则x的取值范围是( )
A.(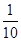 ,1) ,1) | B.(0,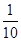 ) ) (1, (1, ) ) |
C.(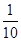 ,10) ,10) | D.(0,1) (10, (10, ) ) |
若函数 在
在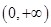 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若函数
 的图象关于直线
的图象关于直线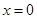 及直线
及直线 对称,且
对称,且 时,
时, ,则
,则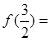 ( )
( )
A. | B. | C. | D. |
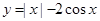 的图象大致是
的图象大致是 
 ,函数
,函数 与
与 的图像可能是( )
的图像可能是( )