题目内容
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
C
解析试题分析:令 =
=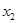 =0,则
=0,则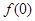 =
=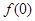
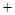
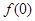
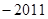 ,f
,f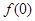 =2011
=2011
令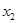 =-
=- ,则 f(0)=f(
,则 f(0)=f( )+f(-
)+f(- )-2011,f(
)-2011,f( )+f(-
)+f(- )=4022
)=4022
因为  在[-2012,2012] 上是单调函数,所以 M+N=4022
在[-2012,2012] 上是单调函数,所以 M+N=4022
考点:抽象最值,赋值法。
点评:充分利用已知条件,合理赋值是解题的关键。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
对于定义域为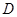 的函数
的函数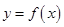 和常数
和常数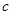 ,若对任意正实数
,若对任意正实数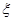 ,
,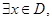 使得
使得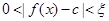 恒成立,则称函数
恒成立,则称函数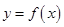 为“敛
为“敛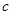 函数”.现给出如下函数:
函数”.现给出如下函数:
①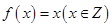 ; ②
; ②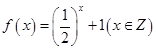 ;
;
③ 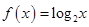 ; ④
; ④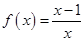 .
.
其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |
函数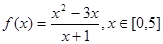 的值域是( )
的值域是( )
| A.[0,2] | B.[0,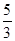 ] ] | C.[-1,2] | D.[-1,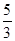 ] ] |
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C.1 | D.3 |
设 用二分法求方程
用二分法求方程 在区间(1,2)上近似解的过程中,计算得到
在区间(1,2)上近似解的过程中,计算得到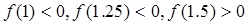 ,则方程的根落在区( )
,则方程的根落在区( )
| A.(1,1.25) | B.(1.25,1.5) | C.(1.5, 1.75) | D.(1.75,2) |
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 ,则
,则 可以是
可以是
A. | B. |
C. | D. |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
下列函数为偶函数,且在 上单调递增的函数是( )
上单调递增的函数是( )
A. | B. | C. | D. |
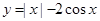 的图象大致是
的图象大致是 