题目内容
17.若${(x-\frac{{\sqrt{a}}}{x^2})^6}$的展开式的常数项为60,则a=4.分析 先求出二项式展开式的通项公式,再令x的系数等于0,求得r的值,即可求得展开式中的常数项的值,再由展开式的常数项为60,求出常数a的值.
解答 解:∵${(x-\frac{{\sqrt{a}}}{x^2})^6}$展开式的通项公式为Tr+1=${C}_{6}^{r}$•x6-r•$(-\sqrt{a})^{r}$•x-2r=$(-\sqrt{a})^{r}$•${C}_{6}^{r}$•x6-3r,
令6-3r=0,可得 r=2,
∴展开式的常数项为$(-\sqrt{a})^{2}•{C}_{6}^{2}$=60,解得a=4.
故答案为:4.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
12.命题“?x0∈∁RQ,x0∈Q”的否定是( )
| A. | ?x0∉∁RQ,x0∈Q | B. | ?x0∈∁RQ,x0∈Q | C. | ?x∉∁RQ,x∉Q | D. | ?x∈∁RQ,x∉Q |
9.函数y=$\frac{1}{2}$x+cosx在x∈[-$\frac{π}{2}$,$\frac{π}{2}$]上的最大值为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
6.已知函数y=2cos(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )
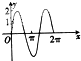

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |