题目内容
5.在平面直角坐标系xOy中,已知直线l的参数方程为:{x=1+ty=2−2t(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2cosθ.直线l与圆相交于A,B两点,求线段AB的长.分析 由直线l的参数方程消去参数t化为直线l的普通方程;圆C的极坐标方程为ρ=2cosθ,即ρ2=2ρcosθ,利用{ρ2=x2+y2x=ρcosθ可把圆C的极坐标方程化为直角坐标方程;利用点到直线的距离公式可得圆心C(1,0)到直线l的距离为d,再利用弦长公式可得|AB|=2√r2−d2.
解答 解:直线l的参数方程为:{x=1+ty=2−2t(t为参数).
消去参数t化为直线l的普通方程为:2x+y-4=0;
圆C的极坐标方程为ρ=2cosθ,即ρ2=2ρcosθ,
∴圆C的z直角坐标方程为:(x-1)2+y2=1;
圆心C(1,0)到直线l的距离为:d=|2−4|√12+22=2√5;
∴|AB|=2√r2−d2=2√1−45=2√55.
点评 本题考查了直线的参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.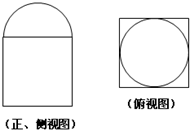 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )| A. | 8+23π | B. | 8+43π | C. | 24+π | D. | 20+2π |
10.若动点A,B分别在直线l1:x+2y-1=0和l2:2x+4y+5=0上移动,则|→OA+→OB|(O为原点)的最小值是( )
| A. | 3√510 | B. | 6√55 | C. | 3√520 | D. | 7√510 |
14.若不等式(-1)na<2+(−1)n+1n对于任意正整数n都成立,则实数a的取值范围是( )
| A. | [−2,32) | B. | (−2,32] | C. | [-3,2] | D. | (-3,1) |
 如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:
如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率: