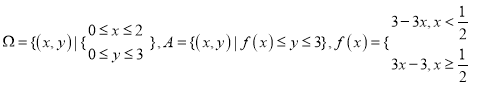Question

【题目】已知函数f（x）＝ex﹣1+alnx．（e为自然对数的底数），λ＝min{a+2，5}．（min{a，b}表示a，b中较小的数．）

（1）当a＝0时，设g（x）＝f（x）﹣x，求函数g（x）在[，]上的最值；

（2）当x1时，证明：f（x）+x2λ（x﹣1）+2．

Answer 1

【答案】（1）最大值为，最小值0；（2）详见解析．

【解析】

（1）当a＝0时，化简，通过g'（x）＝ex﹣1﹣1，令g'（x）＝0，求出极值点，判断函数的单调性，然后求解函数的极值以及函数的最值即可．

（2）①当a+25即a3时，λ＝a+2．f（x）+x2λ（x﹣1）+2ex﹣1+alnx+x2﹣（a+2）x+a0，设k（x）＝ex﹣1+alnx+x2﹣（a+2）x+a，求出导函数，构造函数，通过函数的导数，判断函数的单调性，结合a3，a＞3时，通过函数的最值，转化证明即可．

解:（1）当a＝0时，，

则g'（x）＝ex﹣1﹣1，令g'（x）＝0，得x＝1，

当x1时，g'（x）0；当x1时，g'（x）0，

所以函数g（x）在区间上单调递减，在区间上单调递增，

从而g（x）在上的最小值为g（1）＝0，

因为，，

所以，

从而g（x）在上的最大值为．

（2）①当a+25,即a3时，λ＝a+2．f（x）+x2λ（x﹣1）+2ex﹣1+alnx+x2﹣（a+2）x+a0，

设k（x）＝ex﹣1+alnx+x2﹣（a+2）x+a，

则，

令，

则，

因为x1，

所以x2ex﹣1+2x2＝x2（ex﹣1+2）3，

因为a3，

所以φ'（x）0，当且仅当x＝1且a＝3时，等号成立．

从而k'（x）在[1，+∞）上单调递增．

注意到k'（1）＝1，所以k'（x）0，从而k（x）在[1，+∞）上单调递增，

注意到k（1）＝0，所以k（x）0，原不等式成立．

②当a+25即a＞3时，λ＝5,f（x）+x2λ（x﹣1）+2ex﹣1+alnx+x2﹣5x+30，

由（1）知ex﹣1x，及x1，a3，

所以ex﹣1+alnx+x2﹣5x+33lnx+x2﹣4x+3．

设h（x）＝3lnx+x2﹣4x+3，x1，

则，

所以h（x）在[1，+∞）上单调递增，

注意到h（1）＝0，

所以h（x）0，原不等式成立．

综上，当x1时，不等式f（x）+x2λ（x﹣1）+2成立．