题目内容
【题目】已知函数f(x)=x3﹣ax2+bx+c(a,b,c∈R).
(1)若函数f(x)在x=﹣1和x=3处取得极值,试求a,b的值;
(2)在(1)的条件下,当x∈[﹣2,6]时,f(x)<2|c|恒成立,求c的取值范围.
【答案】(1)![]() ; (2)(-∞,-18)∪(54,+∞).
; (2)(-∞,-18)∪(54,+∞).
【解析】
(1)根据函数的极值的概念得到方程组解出参数值即可;(2)对函数求导得到函数的单调性和极值,进而得到函数的最大值为c+54,要使f(x)<2|c|恒成立,只要c+54<2|c|即可.
(1)f′(x)=3x2-2ax+b,
∵函数f(x)在x=-1和x=3处取得极值,
∴-1,3是方程3x2-2ax+b=0的两根.
∴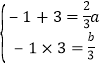 ∴
∴![]() .
.
经检验满足题意.
(2)由(1)知f(x)=x3-3x2-9x+c,
f′(x)=3x2-6x-9.令f′(x)=0,得x=-1或x=3.
当x变化时,f′(x),f(x)随x的变化情况如下表:
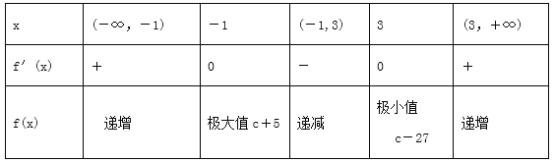
而f(-2)=c-2,f(6)=c+54,
∴当x∈[-2,6]时,f(x)的最大值为c+54,
要使f(x)<2|c|恒成立,只要c+54<2|c|即可,
当c≥0时,c+54<2c,∴c>54 ,
当c<0时,c+54<-2c,∴c<-18.
∴c∈(-∞,-18)∪(54,+∞),此即为实数c的取值范围.

练习册系列答案
相关题目