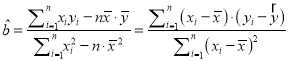题目内容
【题目】当![]() ,则称点
,则称点![]() 为平面上单调格点:设
为平面上单调格点:设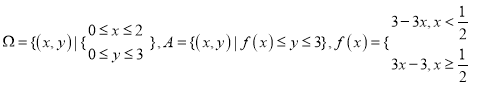
求从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上的概率;
上的概率;
求从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点的概率.
上的格点的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)作出集合![]() 所对应的区域,记事件
所对应的区域,记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”,根据几何概型,利用面积比,即可求解概率;
上”,根据几何概型,利用面积比,即可求解概率;
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”,得出基本事件的总数,和事件
上的格点”,得出基本事件的总数,和事件![]() 所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
试题解析:
作出集合![]() 所对应的区域(如图):
所对应的区域(如图):
矩形![]()
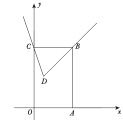
则:(1)记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”
上”
则事件![]() 符合几何概型,即
符合几何概型,即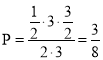 .
.
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”
上的格点”
则事件![]() 符合古典概型,区域
符合古典概型,区域![]() 中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有
中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有![]() 个;而区域
个;而区域![]() 上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
∴![]()

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: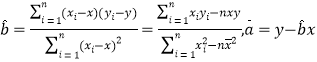 .
.