题目内容
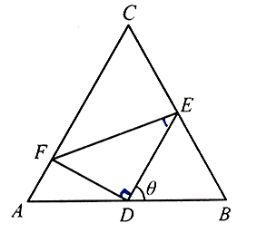
【题目】如图，正三角形ABC的边长为2，D，E，F分别在三边AB，BC和CA上，且D为AB的中点，
，
，
.
（1）当
时，求
的大小；
（2）求
的面积S的最小值及使得S取最小值时的值.
【答案】（1）θ＝60；（2）当θ＝45时，S取最小值
.
【解析】
试题本题主要考查正弦定理、直角三角形中正切的定义、两角和的正弦公式、倍角公式、三角形面积公式等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，在
中，
，①，而在
中，利用正弦定理，用
表示DE，在
中，利用正弦定理，用表示DF，代入到①式中，再利用两角和的正弦公式展开，解出
，利用特殊角的三角函数值求角
；第二问，将第一问得到的DF和DE代入到三角形面积公式中，利用两角和的正弦公式和倍角公式化简表达式，利用正弦函数的有界性确定S的最小值.
在△BDE中，由正弦定理得
，
在△ADF中，由正弦定理得
． 4分
由tan∠DEF＝
，得
，整理得
，
所以θ＝60． 6分
（2）S＝
DE·DF＝
． 10分
当θ＝45时，S取最小值
． 12分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
