题目内容
【题目】若数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}满足![]() ,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+
,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+![]() 对一切n∈N*恒成立,求实数λ的取值范围.
对一切n∈N*恒成立,求实数λ的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]()
【解析】试题分析:(1)数列![]() 满足
满足![]() ,
, ![]() ,且
,且![]() ,可得
,可得![]() ,解得
,解得![]() ,利用等差数列的通项公式可得
,利用等差数列的通项公式可得![]() ,可得
,可得![]() ,化为
,化为![]() ,利用等比数列的通项公式可得
,利用等比数列的通项公式可得![]() ;(2)设数列
;(2)设数列![]() 满足
满足![]() ,利用“错位相减法”可得数列
,利用“错位相减法”可得数列![]() 的前
的前![]() 项和为
项和为![]() ,再利用数列的单调性与分类讨论即可得出.
,再利用数列的单调性与分类讨论即可得出.
试题解析:(1)∵数列![]() 满足
满足![]() ,
, ![]() ,且
,且![]() ,∴
,∴![]() ,解得
,解得![]() ,又数列
,又数列![]() 是公差为2的等差数列,∴
是公差为2的等差数列,∴![]() ,∴
,∴![]() ,化为
,化为![]() ,∴数列
,∴数列![]() 是等比数列,公比为2,∴
是等比数列,公比为2,∴![]() .
.
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,∴
,∴![]() ,∴
,∴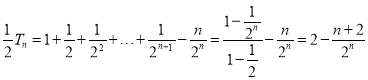 ,∴
,∴![]() ,不等式
,不等式![]() ,化为:
,化为: ![]() ,
, ![]() 时,
时, ![]() ,∴
,∴![]() ;
; ![]() 时,
时, ![]() ,∴
,∴![]() ,综上可得:实数
,综上可得:实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目