题目内容

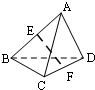
空间四边形ABCD中，AD=BC=2，E，F分别是AB，CD的中点，EF=
3
，则异面直线AD，BC所成的角为（　　）
A．30°B．60°C．90°D．120°
取AC中点G，连接EG、FG，
由三角形中位线的知识可知：EG
∥
.
1
2
BC，FG
∥
.
1
2
AD，
∴∠EGF或其补角即为异面直线AD，BC所成的角，
在△EFG中，cos∠EGF=
EG2+FG2-EF2
2×EG×FG
=
12+12-(
3
)2
2×1×1
=-
1
2
，
∴∠EGF=120°，由异面直线所成角的范围可知应取其补角60°，
故选：B
练习册系列答案
相关题目
如图所示，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，AB=BC=AA1，∠ABC=90°，点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是（　　）
A．45°B．60°C．90°D．120°
如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点，
（Ⅰ）求直线BC与A1C所成的角的度数．
（Ⅱ）求证：A1C∥平面BDE．
如图ABCD-A1B1C1D1是正方体，B1E1=D1F1=
A1B1
4
，则BE1与DF1所成的角的余弦值是（　　）
A．
15
17
B．
1
2
C．
8
17
D．
3
2
如图正方体ABCD-A1B1C1D1中，E，F分别为AB，CC1的中点，则异面直线A1C与EF所成角的余弦值为（　　）
A．
3
3
B．
2
3
C．
1
3
D．
1
6
在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，若AC=BD=a，且AC与BD所成的角为45°，则四边形EFGH的面积为（　　）
A．
2
16
a2		B．
2
8
a2		C．
2
4
a2		D．
2
2
a2
正方体ABCD-A1B1C1D1中，异面直线AC与BD1所成角为______．
如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且DB=DC=2，点E为BC的中点，若直线AE与底面BCD所成的角为45°，则三棱锥A-BCD的体积等于（　　）
A．
2
3
B．
4
3
C．2D．
2
2
3
正方体ABCD-A1B1C1D1中直线A1C1与平面A1BD夹角的余弦值是（　　）
A．
2
4
B．
2
3
C．
3
3
D．
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网