题目内容
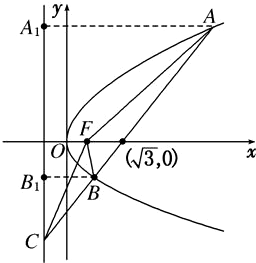
设抛物线y2=2x的焦点为F,过点M(
,0)的直线与抛物线相交于A、B两点,与抛物线的准线相交于点C,|BF|=2,则△BCF与△ACF的面积之比
=( )
| 3 |
| S△BCF |
| S△ACF |
A.
| B.
| C.
| D.
|
如图过B作准线l:x=-
的垂线,垂足分别为A1,B1,
由于F到直线AB的距离为定值.
∴
=
.
又∵△B1BC∽△A1AC、
∴
=
,
由拋物线定义
=
=
.
由|BF|=|BB1|=2知xB=
,yB=-
,
∴AB:y-0=
(x-
).
把x=
代入上式,求得yA=2,xA=2,
∴|AF|=|AA1|=
.
故
=
=
=
.
故选A
| 1 |
| 2 |
由于F到直线AB的距离为定值.
∴
| S△BCF |
| S△ACF |
| |BC| |
| |AC| |
又∵△B1BC∽△A1AC、
∴
| |BC| |
| |AC| |
| |BB1| |
| AA1 |
由拋物线定义
| |BB1| |
| AA1 |
| |BF| |
| |AF| |
| 2 |
| |AF| |
由|BF|=|BB1|=2知xB=
| 3 |
| 2 |
| 3 |
∴AB:y-0=
| ||||
|
| 3 |
把x=
| y2 |
| 2 |
∴|AF|=|AA1|=
| 5 |
| 2 |
故
| S△BCF |
| S△ACF |
| |BF| |
| |AF| |
| 2 | ||
|
| 4 |
| 5 |
故选A


练习册系列答案
相关题目

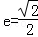 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
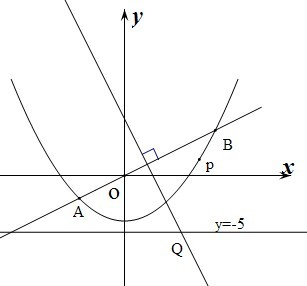
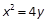 相切于点P(2,1),且与
相切于点P(2,1),且与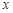 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .
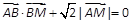 ,求点M的轨迹C;
,求点M的轨迹C;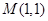 作斜率为
作斜率为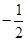 的直线与椭圆
的直线与椭圆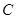 :
: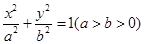 相交于
相交于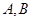 ,若
,若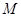 是线段
是线段 的中点,则椭圆
的中点,则椭圆