题目内容
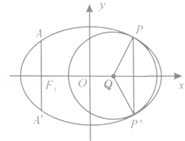
如图,椭圆的中心为原点O,长轴在x轴上,离心率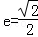 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP'Q的面积S的最大值,并写出对应的圆Q的标准方程.
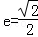 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP'Q的面积S的最大值,并写出对应的圆Q的标准方程.

(1)
(2)见解析

(2)见解析
(1)设椭圆方程为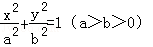 ,
,
左焦点F1(﹣c,0),将横坐标﹣c代入椭圆方程,得y=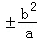 ,
,
所以 ①,
①,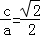 ②,a2=b2+c2③,联立①②③解得a=4,
②,a2=b2+c2③,联立①②③解得a=4, ,
,
所以椭圆方程为: ;
;
(2)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),
则圆Q的方程为:(x﹣t)2+y2=r2,
由 得x2﹣4tx+2t2+16﹣2r2=0,
得x2﹣4tx+2t2+16﹣2r2=0,
由△=0,即16t2﹣4(2t2+16﹣2r2)=0,得t2+r2=8,①
把x=m代入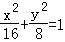 ,得
,得 ,
,
所以点P坐标为(m, ),代入(x﹣t)2+y2=r2,得
),代入(x﹣t)2+y2=r2,得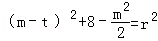 ,②
,②
由①②消掉r2得4t2﹣4mt+m2=0,即m=2t,
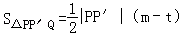 =
= ×(m﹣t)=
×(m﹣t)= =
= ≤
≤ ×
× =2
=2 ,
,
当且仅当4﹣t2=t2即t= 时取等号,
时取等号,
此时t+r= +
+ <4,椭圆上除P、P′外的点在圆Q外,
<4,椭圆上除P、P′外的点在圆Q外,
所以△PP'Q的面积S的最大值为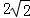 ,圆Q的标准方程为:
,圆Q的标准方程为: .
.
当圆心Q、直线PP′在y轴左侧时,由对称性可得圆Q的方程为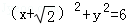 ,△PP'Q的面积S的最大值仍为为
,△PP'Q的面积S的最大值仍为为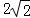 .
.
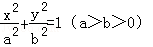 ,
,左焦点F1(﹣c,0),将横坐标﹣c代入椭圆方程,得y=
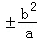 ,
,所以
 ①,
①,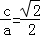 ②,a2=b2+c2③,联立①②③解得a=4,
②,a2=b2+c2③,联立①②③解得a=4, ,
,所以椭圆方程为:
 ;
;(2)设Q(t,0)(t>0),圆的半径为r,直线PP′方程为:x=m(m>t),
则圆Q的方程为:(x﹣t)2+y2=r2,
由
 得x2﹣4tx+2t2+16﹣2r2=0,
得x2﹣4tx+2t2+16﹣2r2=0,由△=0,即16t2﹣4(2t2+16﹣2r2)=0,得t2+r2=8,①
把x=m代入
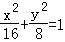 ,得
,得 ,
,所以点P坐标为(m,
 ),代入(x﹣t)2+y2=r2,得
),代入(x﹣t)2+y2=r2,得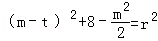 ,②
,②由①②消掉r2得4t2﹣4mt+m2=0,即m=2t,
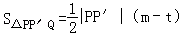 =
= ×(m﹣t)=
×(m﹣t)= =
= ≤
≤ ×
× =2
=2 ,
,当且仅当4﹣t2=t2即t=
 时取等号,
时取等号,此时t+r=
 +
+ <4,椭圆上除P、P′外的点在圆Q外,
<4,椭圆上除P、P′外的点在圆Q外,所以△PP'Q的面积S的最大值为
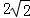 ,圆Q的标准方程为:
,圆Q的标准方程为: .
.当圆心Q、直线PP′在y轴左侧时,由对称性可得圆Q的方程为
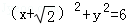 ,△PP'Q的面积S的最大值仍为为
,△PP'Q的面积S的最大值仍为为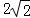 .
.
练习册系列答案
相关题目
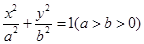 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
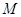 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 ,
,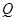 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由. 与椭圆
与椭圆
 相交于A、B两点.
相交于A、B两点.  ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长; 与向量
与向量 互相垂直(其中
互相垂直(其中 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值. 的直线与曲线
的直线与曲线 和
和 都相切,则
都相切,则 等于 ( )
等于 ( ) 或
或

 或
或
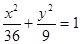 的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
的弦被点(4,2)平分,则这条弦所在的直线方程是 ( )
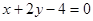
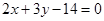

 为双曲线
为双曲线 的左右焦点,点
的左右焦点,点 在
在 上,
上, ,则
,则 ( )
( )


