题目内容
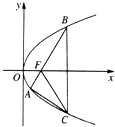
如图,直线y=
x与抛物线y=
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
(1)求点Q的坐标;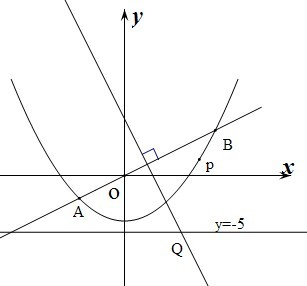
(2)当P为抛物线上位于线段AB下方(含A、B)的动点时,求△OPQ面积的最大值.
| 1 |
| 2 |
| 1 |
| 8 |
(1)求点Q的坐标;

(2)当P为抛物线上位于线段AB下方(含A、B)的动点时,求△OPQ面积的最大值.
(1)解方程组
得
或
即A(-4,-2),B(8,4),
从而AB的中点为M(2,1),
由kAB═
,直线AB的垂直平分线方程y-1=-2(x-2).
令y=-5,得x=5,
∴Q(5,-5).
(2)直线OQ的方程为x+y=0,设P(x,
x2-4).
∵点P到直线OQ的距离
d=
=
|x2+8x-32|.
|OQ|=5
,∴S△OPQ=
|OQ|d=
|x2+8x-32|
∵P为抛物线上位于线段AB下方的点,且P不在直线OQ上,
∴-4≤x<4
-4或4
-4<x≤8.
∵函数y=x2+8x-32在区间[-4,8]上单调递增,
∴当x=8时,△OPQ的面积取到最大值30.
|
|
|
从而AB的中点为M(2,1),
由kAB═
| 1 |
| 2 |
令y=-5,得x=5,
∴Q(5,-5).
(2)直线OQ的方程为x+y=0,设P(x,
| 1 |
| 8 |
∵点P到直线OQ的距离
d=
|x+
| ||
|
| 1 | ||
8
|
|OQ|=5
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
∵P为抛物线上位于线段AB下方的点,且P不在直线OQ上,
∴-4≤x<4
| 3 |
| 3 |
∵函数y=x2+8x-32在区间[-4,8]上单调递增,
∴当x=8时,△OPQ的面积取到最大值30.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,椭圆
中,椭圆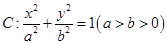 的离心率为
的离心率为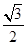 ,直线
,直线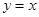 被椭圆
被椭圆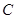 截得的线段长为
截得的线段长为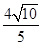 .
.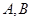 两点(
两点(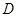 在椭圆
在椭圆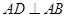 ,直线
,直线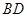 与
与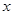 轴、
轴、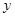 轴分别交于
轴分别交于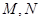 两点.
两点.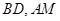 的斜率分别为
的斜率分别为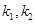 ,证明存在常数
,证明存在常数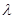 使得
使得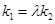 ,并求出
,并求出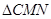 面积的最大值.
面积的最大值.