题目内容
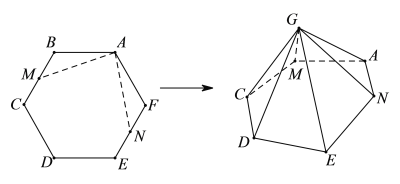
【题目】如图,六边形![]() 的六个内角均相等,
的六个内角均相等,![]() ,M,N分别是线段
,M,N分别是线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() ,现将
,现将![]() ,
,![]() 折起,使得B,F重合于点G,则二面角
折起,使得B,F重合于点G,则二面角![]() 的余弦值的取值范围是______.
的余弦值的取值范围是______.
【答案】![]()
【解析】
由题意结合翻折的性质可得点![]() 只能在
只能在![]() 中点到点
中点到点![]() 之间(包含端点)运动,且二面角在运动的过程中逐渐变小,分别求出点
之间(包含端点)运动,且二面角在运动的过程中逐渐变小,分别求出点![]() 与
与![]() 中点、点
中点、点![]() 重合时二面角的大小即可得解.
重合时二面角的大小即可得解.
由题意,当![]() 在点
在点![]() 和
和![]() 中点之间(不含中点)时,
中点之间(不含中点)时,![]() ,B,F无法重合;
,B,F无法重合;
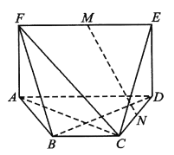
当![]() 为
为![]() 中点时,由
中点时,由![]() ,可知翻折后点
,可知翻折后点![]() 落在平面
落在平面![]() 上,如图:
上,如图:
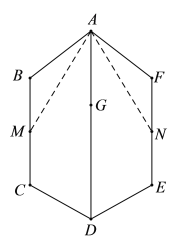
此时二面角![]() 为
为![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,
,
在![]() 从
从![]() 中点向
中点向![]() 运动的过程中,二面角
运动的过程中,二面角![]() 逐渐减小,
逐渐减小,
当![]() 与
与![]() 重合时,过点
重合时,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,如图:
,如图:
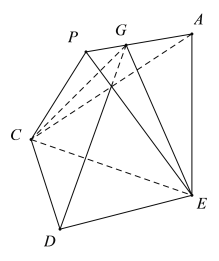
由![]() ≌
≌![]() ,所以
,所以![]() ,
,![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
设![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() .
.
所以二面角![]() 的余弦值的取值范围为
的余弦值的取值范围为![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校课外兴趣小组利用假期到植物园开展社会实践活动,研究某种植物生长情况与温度的关系.现收集了该种植物月生长量y(cm)与月平均气温x(℃)的8组数据,并制成如图所示的散点图.
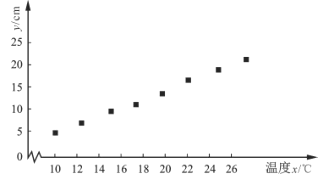
根据收集到的数据,计算得到如下值:
|
|
|
|
18 | 12.325 | 224.04 | 235.96 |
(1)求出y关于x的线性回归方程(最终结果的系数精确到0.01),并求温度为28℃时月生长量y的预报值;
(2)根据y关于x的回归方程,得到残差图如图所示,分析该回归方程的拟合效果.
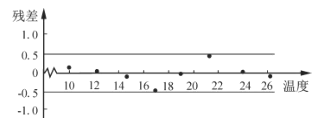
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为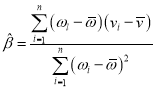 ,
,![]() .
.