题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) ![]() .
.
【解析】试题分析:(1)对函数求导得到![]()
![]() ,讨论
,讨论![]() 和0和1 的大小关系,在不同情况下求得导函数的正负即得到原函数的单调性,根据极值的概念得到结果;(2)设
和0和1 的大小关系,在不同情况下求得导函数的正负即得到原函数的单调性,根据极值的概念得到结果;(2)设![]()
![]() ,构造以上函数,研究函数的单调性,求得函数的最值,使得最小值大于等于0即可.
,构造以上函数,研究函数的单调性,求得函数的最值,使得最小值大于等于0即可.
解析:
(Ⅰ)![]() ,
,
![]()
![]() ,
,
∵![]() 的定义域为
的定义域为![]() .
.
①![]() 即
即![]() 时,
时, ![]() 在
在![]() 上递减,
上递减, ![]() 在
在![]() 上递增,
上递增,
![]() ,
, ![]() 无极大值.
无极大值.
②![]() 即
即![]() 时,
时, ![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]()
![]() ,
, ![]() .
.
③![]() 即
即![]() 时,
时, ![]() 在
在![]() 上递增,
上递增, ![]() 没有极值.
没有极值.
④![]() 即
即![]() 时,
时, ![]() 在
在![]() 和
和![]() 上递增,
上递增, ![]() 在
在![]() 上递减,
上递减,
∴![]() ,
, ![]()
![]() .
.
综上可知: ![]() 时,
时, ![]() ,
, ![]() 无极大值;
无极大值;
![]() 时,
时, ![]()
![]() ,
, ![]() ;
;
![]() 时,
时, ![]() 没有极值;
没有极值;
![]() 时,
时, ![]() ,
, ![]()
![]() .
.
(Ⅱ)设![]()
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
, 
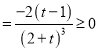 ,
,
∴![]() 在
在![]() 上递增,∴
上递增,∴![]() 的值域为
的值域为![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,
上的增函数,
∴![]() ,适合条件.
,适合条件.
②当![]() 时,∵
时,∵![]() ,∴不适合条件.
,∴不适合条件.
③当![]() 时,对于
时,对于![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
存在![]() ,使得
,使得![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
即在![]() 时,
时, ![]() ,∴不适合条件.
,∴不适合条件.
综上, ![]() 的取值范围为
的取值范围为![]() .
.

【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
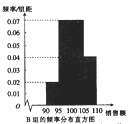
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.