Question

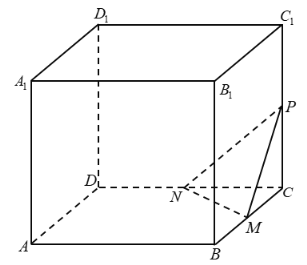
【题目】如图，在棱长为1的正方体中，为棱上的动点（点不与点，重合），过点作平面分别与棱，交于，两点，若，则下列说法正确的是（ ）

A.面

B.存在点，使得∥平面

C.存在点，使得点到平面的距离为

D.用过，，三点的平面去截正方体，得到的截面一定是梯形

Answer 1

【答案】ACD

【解析】

利用空间直线平面的位置关系对A,B分析判断，利用点到平面的距离和截面知识对C,D分析判断得解.

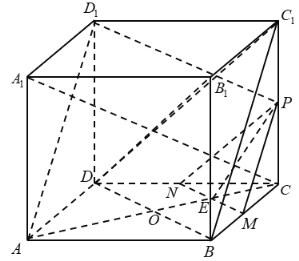
A.如图所示，平面 平面,在正方体中，平面,所以平面，所以选项A正确；

B.假设存在点，使得∥平面，因为平面,平面平面=PE,所以,所以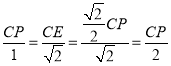,显然不等，所以假设不成立，故选项B错误；

C. 当CP越小，则点到平面的距离越大，这个距离大于零且无限接近,所以存在点，使得点到平面的距离为，所以选项C正确；

D. 用过，，三点的平面去截正方体，因为PM//,所以得到的截面就是平面,它是一个梯形，所以该选项正确.

故选：ACD