题目内容
【题目】关于函数f（x）=
有如下四个命题：
①f（x）的图像关于y轴对称．
②f（x）的图像关于原点对称．
③f（x）的图像关于直线x=
对称．
④f（x）的最小值为2．
其中所有真命题的序号是__________．
【答案】②③
【解析】
利用特殊值法可判断命题①的正误；利用函数奇偶性的定义可判断命题②的正误；利用对称性的定义可判断命题③的正误；取
可判断命题④的正误.综合可得出结论.
对于命题①，
，
，则
，
所以，函数
的图象不关于
轴对称，命题①错误；
对于命题②，函数的定义域为
，定义域关于原点对称，
，
所以，函数的图象关于原点对称，命题②正确；
对于命题③，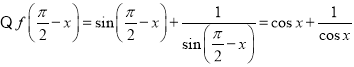
，
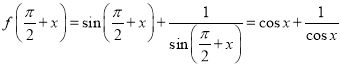，则
，
所以，函数的图象关于直线
对称，命题③正确；
对于命题④，当时，
，则
，
命题④错误.
故答案为：②③.
培优三好生系列答案
优化作业上海科技文献出版社系列答案
【题目】为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为
.2015年开始，全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占 2019 年贫困户总数的比）及该项目的脱贫率见下表：
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的（ ）
A.
B.
C.
D.
【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：
锻炼人次 空气质量等级 | [0，200] | (200，400] | (400，600] |
1（优） | 2 | 16 | 25 |
2（良） | 5 | 10 | 12 |
3（轻度污染） | 6 | 7 | 8 |
4（中度污染） | 7 | 2 | 0 |
（1）分别估计该市一天的空气质量等级为1，2，3，4的概率；
（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；
（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附：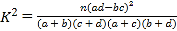
，
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】“网购”已经成为我们日常生活中的一部分，某地区随机调查了100名男性和100名女性在“双十一”活动中用于网购的消费金额，数据整理如下：
男性消费金额频数分布表
消费金额 （单位：元） | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人数 | 15 | 15 | 20 | 30 | 20 |
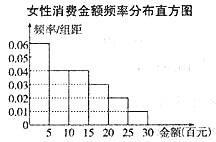
（1）试分别计算男性、女性在此活动中的平均消费金额；
（2）如果分别把男性、女性消费金额与中位数相差不超过200元的消费称作理性消费，试问是否有5成以上的把握认为理性消费与性别有关.
附：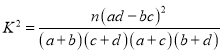
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
