题目内容
【题目】已知
，
，
，
：
，
：
.给出以下四个命题：
①分别过点
，
，作的不同于
轴的切线，两切线相交于点
，则点的轨迹为椭圆的一部分；
②若，相切于点
，则点的轨迹恒在定圆上；
③若，相离，且
，则与，都外切的圆的圆心在定椭圆上；
④若，相交，且
，则与，一个内切一个外切的圆的圆心的轨迹为椭圆的一部分.
则以上命题正确的是__________.
【答案】①②④
【解析】
由圆与圆的位置关系和椭圆、双曲线的定义，逐一判断可得答案.
对于①，如图所示，
，
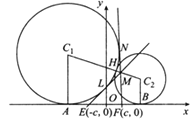
故点M恒在以E，F为焦点，AB为长轴的椭圆上，①正确；
对于②，若
与x轴相切于点A，
与x轴相切于点B，由题意知
相外切，且，相切于点H，过点H作两圆公切线，交x轴于点Q，如图所示，
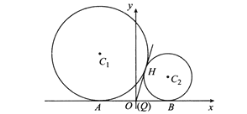
则
，故Q与O点重合，所以
，故点H的轨迹恒在定圆上，②正确；
对于③设与，都相切的圆的圆心为T，半径为r，则T满足
，
，得到
，故圆心T的轨迹是双曲线的一部分，③不正确，
对于④设与，一个内切一个外切的圆的圆心为P，半径为r，则点P满足
，
，所以
，所以点P的轨迹为椭圆的一部分. ④正确.
故答案为：①②④
练习册系列答案
相关题目
