题目内容
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程;
(2)已知P是曲线C上的一动点,过点P作直线![]() 交直线于点A,且直线
交直线于点A,且直线![]() 与直线l的夹角为45°,若
与直线l的夹角为45°,若![]() 的最大值为6,求a的值.
的最大值为6,求a的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用两角差的余弦公式把![]() 展开,结合
展开,结合![]() ,
,![]() 可得直线
可得直线![]() 的直角坐标方程;
的直角坐标方程;
(2)依题意可知曲线C的参数方程为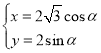 (
(![]() 为参数),设
为参数),设![]() ,写出点
,写出点![]() 到直线
到直线![]() 的距离,利用三角函数求其最大值,可得
的距离,利用三角函数求其最大值,可得![]() 的最大值,结合已知列式求解
的最大值,结合已知列式求解![]() 即可.
即可.
(1)由![]() ,得
,得![]() ,
,
即![]() .
.
∵![]() ,
,![]() ,
,
∴直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() .
.
(2)依题意可知曲线![]() 的参数方程为
的参数方程为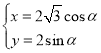 (
(![]() 为参数).
为参数).
设![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为:
的距离为:
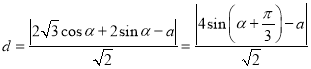 .
.
∵![]() ,
,
∴当![]() 时,
时,![]() .
.
又过点![]() 作直线
作直线![]() 交直线于点A,且直线
交直线于点A,且直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() 的最大值为
的最大值为![]() ,即
,即![]() .
.
∵![]() ,∴解得
,∴解得![]() .
.

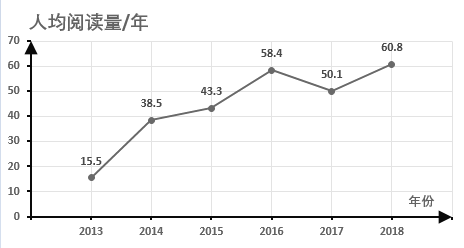
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
【题目】某农场更新技术培育了一批新型的“盆栽果树”,这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性,能够一年四季都有花、四季都结果.现为了了解果树的结果情况,从该批果树中随机抽取了容量为120的样本,测量这些果树的高度(单位:厘米),经统计将所有数据分组后得到如图所示的频率分布直方图.
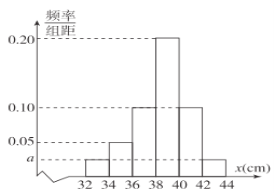
(1)求![]() ;
;
(2)已知所抽取的样本来自![]() 两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
(i)请将图中列联表补充完整,并判断是否有![]() 的把握认为“优品盆栽”与
的把握认为“优品盆栽”与![]() 两个实验基地有关?
两个实验基地有关?
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
(ii)用样本数据来估计这批果树的生长情况,若从该农场培育的这批“盆栽果树”中随机抽取4棵,求其中“优品盆栽”的棵树![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]() .
.