题目内容
【题目】已知命题p:“方程:![]() 表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
【答案】(1)(﹣2,0)∪(0,2) (2)(﹣2,﹣1)∪(1,2)∪{0}
【解析】
(1)由题意可得关于![]() 的不等式组,求解得答案;
的不等式组,求解得答案;
(2)求出命题![]() 为真命题的
为真命题的![]() 的取值范围,由“
的取值范围,由“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,可得
”为假命题,可得![]() 真
真![]() 假,或
假,或![]() 假
假![]() 真.然后利用交、并、补集的混合运算求解.
真.然后利用交、并、补集的混合运算求解.
解:(1)![]() 方程:
方程:![]() 表示焦点在
表示焦点在![]() 轴上的双曲线,
轴上的双曲线,
![]()
![]() ,解得
,解得![]() 或
或![]() .
.
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)当命题![]() 为真时,
为真时,![]() ,解得
,解得![]() .
.
![]() “
“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,
”为假命题,
![]() 真
真![]() 假,或
假,或![]() 假
假![]() 真.
真.
若![]() 真
真![]() 假,则
假,则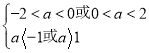 ,解得
,解得![]() 或
或![]() ;
;
若![]() 假
假![]() 真,则
真,则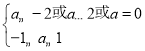 ,解得
,解得![]() .
.
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

