题目内容
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆![]() 与椭圆
与椭圆![]() 是相似的两个椭圆,并且相交于上下两个顶点,椭圆
是相似的两个椭圆,并且相交于上下两个顶点,椭圆![]() 的长轴长是4,椭圆
的长轴长是4,椭圆![]() 长轴长是2,点
长轴长是2,点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左焦点与右焦点.
的左焦点与右焦点.

(1)求椭圆![]() ,
,![]() 的方程;
的方程;
(2)过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程是
的方程是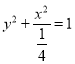 (2)
(2)![]()
【解析】
(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,椭圆
,椭圆![]() 的半焦距为
的半焦距为![]() ,直接利用椭圆的定义得到答案.
,直接利用椭圆的定义得到答案.
(2)设直线的方程为![]() ,联立方程得到
,联立方程得到![]() ,
,
![]() ,
,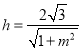 ,
,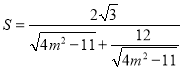 利用均值不等式得到答案.
利用均值不等式得到答案.
解:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,椭圆
,椭圆![]() 的半焦距为
的半焦距为![]() ,由已知
,由已知![]() ,
,![]() =1,
=1,
∵椭圆![]() 与椭圆
与椭圆![]() 的离心率相等,即
的离心率相等,即![]() ,
,
∴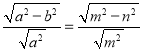 ,即
,即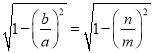 ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程是
的方程是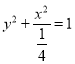 ;
;
(2)显然直线的斜率不为0,故可设直线的方程为![]() .
.
联立: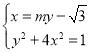 ,得
,得![]() ,即
,即![]() ,
,
∴![]() ,设
,设![]() ,
,![]() ,
,
则![]() ,
,![]() ,∴
,∴![]() ,
,
![]() 的高即为点
的高即为点![]() 到直线
到直线![]() :
:![]() 的距离
的距离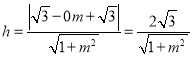 ,
,
∴![]() 的面积
的面积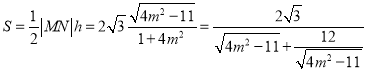 ,
,
∵![]() ,等号成立当且仅当
,等号成立当且仅当![]() ,即
,即![]() 时成立
时成立
∴![]() ,即
,即![]() 的面积的最大值为
的面积的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某单位开展岗前培训期间,甲、乙2人参加了5次考试,成绩统计如下:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩 | 82 | 82 | 79 | 95 | 87 |
乙的成绩 | 95 | 75 | 80 | 90 | 85 |
(1)根据有关统计知识回答问题:若从甲、乙2人中选出1人上岗,你认为选谁合适?请说明理由;
(2)根据有关概率知识解答以下问题:若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”.由上述5次成绩统计,任意抽查两次考试,求至少有一次考试两人“水平相当”的概率.

