Question

【题目】已知复数，其中为虚数单位，对于任意复数，有，．

（1）求的值；

（2）若复数满足，求的取值范围；

（3）我们把上述关系式看作复平面上表示复数的点和表示复数的点之间的一个变换，问是否存在一条直线，若点在直线上，则点仍然在直线上？如果存在，求出直线的方程，否则，说明理由．

Answer 1

【答案】（1）2；（2）；（3）存在，直线方程，理由见解析

【解析】

（1）利用复数的模的性质即可得解；

（2）利用复数的几何意义即可得解；

（3）设，，由，得，① 设存在直线，则直线一定过原点，故设直线的方程为，② ，联立化简即可得解.

（1）因为，所以，

故，所以，

又，

故；

（2）由，得复数的轨迹是点，的中垂线，

又,

所以，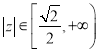

即，

故的取值范围为；

（3）设，，

由，得，①

设存在直线满足题意，则直线一定过原点，故设直线的方程为，②

由题意知：把①代入②可得，③

把②代入③可得，解得，

故存在直线，其方程为.