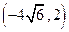题目内容
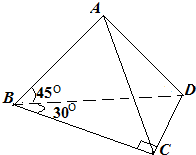
已知如图,平面ABD⊥平面BCD,∠BAD=∠BCD=90°,∠ABD=45°,∠CBD=30°.
(Ⅰ)异面直线AB、CD所成的角为α,异面直线AC、BD所成的角为β,求证:α=β;
(Ⅱ)求二面角B-AC-D的余弦值的绝对值.
(Ⅰ)异面直线AB、CD所成的角为α,异面直线AC、BD所成的角为β,求证:α=β;
(Ⅱ)求二面角B-AC-D的余弦值的绝对值.

(Ⅰ)证明:设BD的中点为O,∠BAD=90°,∠ABD=45°,∴∠BDA=45°,即AB=AD,∴AO⊥BD.
∵平面ABD⊥平面BCD,∴AO⊥面BCD.
以过O点垂直于BD的直线为x轴,以直线BD为y轴,以直线OA为z,建立如图所示的空间直角坐标系A-xyz,设|
|=4.
∴A(0,0,2),B(0,-2,0),C(
,1,0),D(0,2,0),
∴
=(0,-2,-2),
=(
,1,-2),
=(-
,1,0),
=(0,4,0),
∴cosα=|
|=
=
,cosβ=|
|=
=
.
∵0°<α,β≤90°,∴α=β.…6分
(Ⅱ)设
=(x1,y1,z1),
=(x2,y2,z2)分别是平面ABC、平面ACD一个法向量,
∴
⊥
,
⊥
,即
•
=
•
=0,
∴-2y1-2z1=0,
x1+y1-2z1=0,不妨取x1=-
,得
=(-
,1,-1).
同理可求得
=(1,
,
),
∴cos<
,
>=
=
=-
,
所以二面角B-AC-D的余弦值的绝对值为
.…12分.

∵平面ABD⊥平面BCD,∴AO⊥面BCD.
以过O点垂直于BD的直线为x轴,以直线BD为y轴,以直线OA为z,建立如图所示的空间直角坐标系A-xyz,设|
| BD |
∴A(0,0,2),B(0,-2,0),C(
| 3 |
∴
| AB |
| AC |
| 3 |
| CD |
| 3 |
| BD |
∴cosα=|
| ||||
|
|
| 2 | ||
2
|
| ||
| 4 |
| ||||
|
|
| 4 | ||
2
|
| ||
| 4 |
∵0°<α,β≤90°,∴α=β.…6分
(Ⅱ)设
| m1 |
| m2 |
∴
| m1 |
| AB |
| m1 |
| . |
| AC |
| m1 |
| AB |
| m1 |
| . |
| AC |
∴-2y1-2z1=0,
| 3 |
| 3 |
| m1 |
| 3 |
同理可求得
| m2 |
| 3 |
| 3 |
∴cos<
| m1 |
| m2 |
| ||||
|
|
-
| ||||
|
| ||
| 35 |
所以二面角B-AC-D的余弦值的绝对值为
| ||
| 35 |


练习册系列答案
相关题目

 的三个顶点A、B、C,下列命题正确的个数是( )
的三个顶点A、B、C,下列命题正确的个数是( )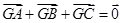 ,则G是
,则G是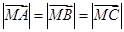 ,点M是
,点M是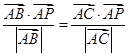 ,则点P在边BC的垂线上;
,则点P在边BC的垂线上;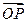 按逆时针旋转
按逆时针旋转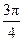 后,得向量
后,得向量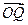 ,则点
,则点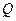 的坐标是( )
的坐标是( )